题目内容
12.一个几何体被切割后剩下部分的几何体的三视图如图所示,则该几何体的表面积为( )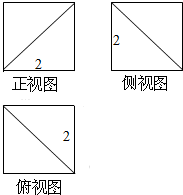
| A. | 18 | B. | 20 | C. | $18+2\sqrt{3}$ | D. | $18+4\sqrt{3}$ |
分析 画出几何体的图形,利用三视图的数据,求解几何体的表面积即可.
解答  解:如图所示,S表=3个全等正方形的面积+3个全等等
解:如图所示,S表=3个全等正方形的面积+3个全等等
腰直角三角形的面积+1个等边三角形的面积=3×2×
2+3×$\frac{1}{2}$×2×2+$\frac{1}{2}$×2$\sqrt{2}$×2$\sqrt{2}$×$\frac{{\sqrt{3}}}{2}$=18+2$\sqrt{3}$,
故选C.
点评 本题考查几何体的三视图,复原几何体,求解几何体的表面积的方法,考查计算能力.

练习册系列答案
相关题目
20.下列函数中,随x的增大,其增大速度最快的是( )
| A. | y=0.001ex | B. | y=1000lnx | C. | y=x1000 | D. | y=1000•2x |
1.设F1,F2分别为双曲线C的左右焦点,直线l过F2且与C的右支交于A,B两点,若△F1AB为直角三角形,且|F1A|,|AB|,|F1B|成等差数列,则双曲线C的离心率为( )
| A. | $\sqrt{10}$ | B. | $\frac{\sqrt{10}}{2}$ | C. | $\frac{\sqrt{10}}{3}$ | D. | $\frac{2\sqrt{10}}{5}$ |
17.已知g(x)=ex(cosx+a)(a∈R)是R上的增函数,则实数a的取值范围为( )
| A. | [2,+∞) | B. | (2,+∞) | C. | [$\sqrt{2}$,+∞) | D. | ($\sqrt{2}$,+∞) |
4.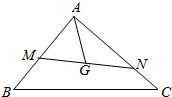 如图所示,已知点G是△ABC的重心,过点G作直线与AB,AC两边分别交于M,N两点,且$\overrightarrow{AM}$=x$\overrightarrow{AB}$,$\overrightarrow{AN}$=y$\overrightarrow{AC}$,则x+2y的最小值为( )
如图所示,已知点G是△ABC的重心,过点G作直线与AB,AC两边分别交于M,N两点,且$\overrightarrow{AM}$=x$\overrightarrow{AB}$,$\overrightarrow{AN}$=y$\overrightarrow{AC}$,则x+2y的最小值为( )
 如图所示,已知点G是△ABC的重心,过点G作直线与AB,AC两边分别交于M,N两点,且$\overrightarrow{AM}$=x$\overrightarrow{AB}$,$\overrightarrow{AN}$=y$\overrightarrow{AC}$,则x+2y的最小值为( )
如图所示,已知点G是△ABC的重心,过点G作直线与AB,AC两边分别交于M,N两点,且$\overrightarrow{AM}$=x$\overrightarrow{AB}$,$\overrightarrow{AN}$=y$\overrightarrow{AC}$,则x+2y的最小值为( )| A. | 2 | B. | $\frac{1}{3}$ | C. | $\frac{{3+2\sqrt{2}}}{3}$ | D. | $\frac{3}{4}$ |
2.在△ABC中,a=2$\sqrt{3},b=3\sqrt{2},cosC=\frac{1}{3}$,则△ABC的面积为( )
| A. | 3$\sqrt{3}$ | B. | 2$\sqrt{3}$ | C. | 4$\sqrt{3}$ | D. | $\sqrt{3}$ |
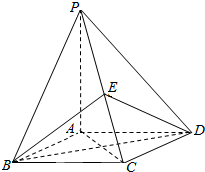 如图4,四边形ABCD为菱形,∠ABC=60°.PA⊥平面ABCD,E为PC中点.
如图4,四边形ABCD为菱形,∠ABC=60°.PA⊥平面ABCD,E为PC中点.