题目内容
（1）已知a＞0，b＞0，比较a3+b3与a2b+ab2的大小；
（2）已知a，b，c是三个不全等的正数，求证：
+
+
＞6．
（2）已知a，b，c是三个不全等的正数，求证：
| b+c |
| a |
| a+c |
| b |
| a+b |
| c |
考点：不等式的证明
专题：综合题,不等式的解法及应用
分析：（1）将两个式子作差变形，通过提取公因式化为完全平方与一个常数的积的形式，判断符号，得出大小关系；
（2）利用分析法证明即可．
（2）利用分析法证明即可．
解答：
（1）解：（a3+b3）-（a2b+ab2）=（a3-a2b）+（b3-ab2）=（a+b）（a-b）2
又∵a＞0，b＞0，∴a+b＞0，而（a-b）2≥0．
∴（a+b）（a-b）2≥0．
故（a3+b3）-（a2b+ab2）≥0，即a3+b3≥a2b+ab2；
（2）证明：要证明：
+
+
＞6，
只需证明：（a+b+c）（
+
+
）＞9，
只需证明：3+
+
+
+
+
+
＞9，
只需证明：
+
+
+
+
+
＞6，
∵
+
≥2，
+
≥2，
+
≥2，a，b，c是三个不全等的正数，
∴
+
+
+
+
+
＞6，
∴
+
+
＞6．
又∵a＞0，b＞0，∴a+b＞0，而（a-b）2≥0．
∴（a+b）（a-b）2≥0．
故（a3+b3）-（a2b+ab2）≥0，即a3+b3≥a2b+ab2；
（2）证明：要证明：
| b+c |
| a |
| a+c |
| b |
| a+b |
| c |
只需证明：（a+b+c）（
| 1 |
| a |
| 1 |
| b |
| 1 |
| c |
只需证明：3+
| b |
| a |
| a |
| b |
| c |
| a |
| a |
| c |
| c |
| b |
| b |
| c |
只需证明：
| b |
| a |
| a |
| b |
| c |
| a |
| a |
| c |
| c |
| b |
| b |
| c |
∵
| b |
| a |
| a |
| b |
| c |
| a |
| a |
| c |
| c |
| b |
| b |
| c |
∴
| b |
| a |
| a |
| b |
| c |
| a |
| a |
| c |
| c |
| b |
| b |
| c |
∴
| b+c |
| a |
| a+c |
| b |
| a+b |
| c |
点评：用作差的方法比较两个式子的大小，注意将差化为因式积的形式，以便于判断符号．
练习册系列答案
相关题目
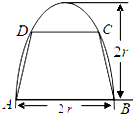如图，有一块半椭圆形钢板，其长半轴长为2r，短半轴长为r，计划将此钢板切割成等腰梯形的形状，下底AB是半椭圆的短轴，上底CD的端点在椭圆上，记CD=2x，梯形面积为S．
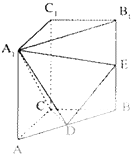直三棱柱ABC-A1B1C1中，AC=CB=AA1=2，∠ACB=90°，E是BB1的中点，D∈AB，∠A1DE=90°． 