题目内容
15.对于实数a,b,定义运算“□”:a□b=$\left\{\begin{array}{l}{{a}^{2}-ab,a≤b}\\{{b}^{2}-ab,a>b}\end{array}\right.$设f(x)=(x-4)□($\frac{7}{4}$x-4),若关于x的方程|f(x)-m|=1(m∈R)恰有四个互不相等的实数根,则实数m的取值范围是(-1,1)∪(2,4).分析 根据新定义得出f(x)的解析式,作出f(x)的函数图象,则f(x)与y=m±1共有4个交点,根据图象列出不等式组解出.
解答 解:解不等式x-4≤$\frac{7}{4}x$-4得x≥0,f(x)=$\left\{\begin{array}{l}{-\frac{3}{4}{x}^{2}+3x,x≥0}\\{\frac{21}{16}{x}^{2}-3x,x<0}\end{array}\right.$,
画出函数f(x)的大致图象如图所示.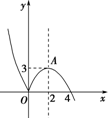
因为关于x的方程|f(x)-m|=1(m∈R),即f(x)=m±1(m∈R)恰有四个互不相等的实数根,
所以两直线y=m±1(m∈R)与曲线y=f(x)共有四个不同的交点,
∴$\left\{\begin{array}{l}{m+1>3}\\{0<m-1<3}\end{array}\right.$或$\left\{\begin{array}{l}{1<m+1<3}\\{m-1<0}\end{array}\right.$或$\left\{\begin{array}{l}{m+1=3}\\{m-1=0}\end{array}\right.$,
解得2<m<4或-1<m<1.
故答案为(-1,1)∪(2,4).
点评 本题考查了函数零点与函数图象的关系,属于中档题.

练习册系列答案
相关题目
3.等腰直角三角形ABC中,∠C=90°,AC=BC=2,点P是△ABC斜边上任意一点,则线段CP的长度不大于$\sqrt{3}$的概率是( )
| A. | $\frac{{\sqrt{2}}}{2}$ | B. | $\frac{{\sqrt{2}}}{4}$ | C. | $\frac{1}{2}$ | D. | $\frac{{\sqrt{6}}}{4}$ |
10.已知三棱锥P-ABC的各顶点都在同一球的面上,且PA⊥平面ABC,若球O的体积为$\frac{20\sqrt{5}π}{3}$(球的体积公式为$\frac{4π}{3}$R3,其中R为球的半径),AB=2,AC=1,∠BAC=60°,则三棱锥P-ABC的体积为( )
| A. | $\frac{\sqrt{3}}{3}$ | B. | $\frac{2\sqrt{3}}{3}$ | C. | $\sqrt{3}$ | D. | $\frac{4\sqrt{3}}{3}$ |
20.已知命题p:?x∈(1,+∞),x3+16>8x,则命题p的否定为( )
| A. | ?x∈(1,+∞),x3+16≤8x | B. | ?x∈(1,+∞),x3+16<8x | ||
| C. | ?x∈(1,+∞),x3+16≤8x | D. | ?x∈(1,+∞),x3+16<8x |
7.阅读程序框图,该算法的功能是输出( )
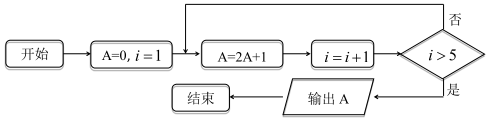

| A. | 数列{2n-1}的前 4项的和 | B. | 数列{2n-1}的第4项 | ||
| C. | 数列{2n}的前5项的和 | D. | 数列?{2n-1}的第5项 |
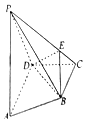 如图,四棱锥P-ABCD中,AD∥BC,AD⊥DC,AD=2BC=2,在侧面PAD中,PA=PD,E为侧棱PC上不同于端点的任意一点且PA⊥DE.
如图,四棱锥P-ABCD中,AD∥BC,AD⊥DC,AD=2BC=2,在侧面PAD中,PA=PD,E为侧棱PC上不同于端点的任意一点且PA⊥DE.