题目内容
10.已知三棱锥P-ABC的各顶点都在同一球的面上,且PA⊥平面ABC,若球O的体积为$\frac{20\sqrt{5}π}{3}$(球的体积公式为$\frac{4π}{3}$R3,其中R为球的半径),AB=2,AC=1,∠BAC=60°,则三棱锥P-ABC的体积为( )| A. | $\frac{\sqrt{3}}{3}$ | B. | $\frac{2\sqrt{3}}{3}$ | C. | $\sqrt{3}$ | D. | $\frac{4\sqrt{3}}{3}$ |
分析 如图所示,在△ABC中,AB=2,AC=1,∠BAC=60°,利用余弦定理可得:BC=$\sqrt{3}$,利用勾股定理的逆定理可得∠ACB=90°.取AB的中点D,则球心O满足OD⊥平面ABC.又PA⊥平面ABC,可得三棱锥P-ABC的外接球的球心O为PB的中点.OD=$\frac{1}{2}$PA.由球的体积计算公式可得:$\frac{4π}{3}$R3=$\frac{20\sqrt{5}π}{3}$,解得R.OD=$\sqrt{{R}^{2}-A{D}^{2}}$,利用三棱锥P-ABC的体积V=$\frac{1}{3}×{S}_{△ABC}×$PA即可得出.
解答 解:如图所示, 在△ABC中,AB=2,AC=1,∠BAC=60°,则BC2=22+12-2×1×2×cos60°=3,
在△ABC中,AB=2,AC=1,∠BAC=60°,则BC2=22+12-2×1×2×cos60°=3,
解得BC=$\sqrt{3}$,∴${1}^{2}+(\sqrt{3})^{2}={2}^{2}$.
∴∠ACB=90°.
取AB的中点D,则球心O满足OD⊥平面ABC.
又PA⊥平面ABC,∴三棱锥P-ABC的外接球的球心O为PB的中点.
∴OD=$\frac{1}{2}$PA.
由球的体积计算公式可得:$\frac{4π}{3}$R3=$\frac{20\sqrt{5}π}{3}$,解得R=$\sqrt{5}$.
∴OD=$\sqrt{{R}^{2}-A{D}^{2}}$=2.
∴PA=4
∴三棱锥P-ABC的体积V=$\frac{1}{3}×{S}_{△ABC}×$PA=$\frac{1}{3}×\frac{1}{2}×1×\sqrt{3}×4$=$\frac{2\sqrt{3}}{3}$.
故选:B.
点评 本题考查了空间位置关系、线面垂直的判定与性质定理、三棱锥的体积计算公式、勾股定理与逆定理、三角形中位线定理、球的体积计算公式,考查了推理能力与计算能力,属于中档题.

 阅读快车系列答案
阅读快车系列答案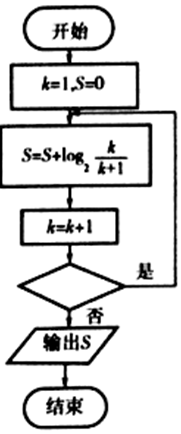
| A. | k<2 | B. | k<3 | C. | k<4 | D. | k<5 |