题目内容
（文）已知cosα=-
，且α为第三象限角，求sinα，tanα的值．
| 4 |
| 5 |
考点：同角三角函数基本关系的运用
专题：三角函数的求值
分析：由cosα的值及α为第三象限角，利用同角三角函数间的基本关系求出sinα与tanα的值即可．
解答：
解：∵cosα=-
，且α为第三象限角，
∴sinα=-
=-
，
则tanα=
=
．
| 4 |
| 5 |
∴sinα=-
| 1-cos2α |
| 3 |
| 5 |
则tanα=
| sinα |
| cosα |
| 3 |
| 4 |
点评：此题考查了同角三角函数基本关系的运用，熟练掌握基本关系是解本题的关键．
练习册系列答案
名校课堂系列答案
相关题目
（
-2x2）5的展开式中常数项是（ ）
| 1 | ||
|
| A、-5 | B、5 | C、-10 | D、10 |
若点O和点F分别为椭圆
+y2=1的中心和左焦点，点P为椭圆上的任意一点，则
•
的最大值为（ ）
| x2 |
| 2 |
| OP |
| FP |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
下列函数中，既是奇函数，又在（0，+∞）上是减函数的是（ ）
A、y=
| ||
| B、y=x2 | ||
| C、y=x | ||
| D、y=-x+1 |
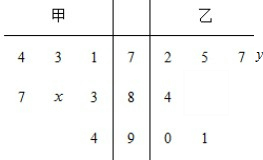某中学高二年级的甲、乙两个班中，需根据某次数学预赛成绩选出某一班的7名学生参加数学竞赛决赛，已知这次预赛他们取得的成绩（满分100分）的茎叶图如图所示，其中甲班7名学生成绩的平均分是81，乙班7名学生成绩的中位数是78． 
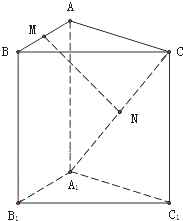在三棱柱ABC-A1B1C1中，M、N分别是AB、A1C的中点，求证：MN∥平面BCB1C1．