题目内容
已知双曲线C：
-
=1（a＞0，b＞0）的离心率为
，且过点（
，-2），则C的实轴长为（ ）
| x2 |
| a2 |
| y2 |
| b2 |
| 3 |
| 3 |
| A、2 | ||
| B、2 | ||
C、
| ||
D、2
|
考点：双曲线的简单性质
专题：计算题,圆锥曲线的定义、性质与方程
分析：利用双曲线C：
-
=1（a＞0，b＞0）的离心率为
，且过点（
，-2），建立方程，即可求出C的实轴长．
| x2 |
| a2 |
| y2 |
| b2 |
| 3 |
| 3 |
解答：
解：∵双曲线C：
-
=1（a＞0，b＞0）的离心率为
，且过点（
，-2），
∴
=
，
-
=1，
∴a=1，
∴C的实轴长为2
故选：B．
| x2 |
| a2 |
| y2 |
| b2 |
| 3 |
| 3 |
∴
| c |
| a |
| 3 |
| 3 |
| a2 |
| 4 |
| b2 |
∴a=1，
∴C的实轴长为2
故选：B．
点评：本题考查双曲线的简单性质，考查学生的计算能力，比较基础．
练习册系列答案
100分闯关期末冲刺系列答案
名校联盟快乐课堂系列答案
相关题目
设a＞0，b＞0，则以下不等式中不恒成立的是（ ）
A、（a+b）（
| ||||||
| B、a2+b2+2≥2a+2b | ||||||
| C、a3+a2b≥ab2+b3 | ||||||
D、
|
函数f（x）=
的定义域为（ ）
| 1 | ||||
|
| A、（2，+∞） | ||
| B、（0，2） | ||
| C、（-∞，2） | ||
D、（0，
|
已知圆x（x-1）+y（y-1）=0与圆x2+y2=r2（r＞
）相内切，则r等于（ ）
| 1 |
| 2 |
A、
| ||||
| B、1 | ||||
C、
| ||||
D、
|
已知函数f（x）=x（lnx-
ax）有两个极值点，则实数a的取值范围是（ ）
| 1 |
| 2 |
| A、（-∞，0） | ||
B、（0，
| ||
| C、（0，1） | ||
| D、（0，+∞） |
观察下列式子：1+
＜
，1+
+
＜
，1+
+
+
＜
，…，根据以上式子可以猜想：1+
+
+…+
＜（ ）
| 1 |
| 22 |
| 3 |
| 2 |
| 1 |
| 22 |
| 1 |
| 32 |
| 5 |
| 3 |
| 1 |
| 22 |
| 1 |
| 32 |
| 1 |
| 42 |
| 7 |
| 4 |
| 1 |
| 22 |
| 1 |
| 32 |
| 1 |
| 20142 |
A、
| ||
B、
| ||
C、
| ||
D、
|
已知“整数对”按如下规律排成一列：（1，1），（1，2），（2，1），（1，3），（2，2），（3，1），（1，4），（2，3），（3，2），（4，1），…，则第58个数对是（ ）
| A、（2，10） |
| B、（3，9） |
| C、（5，7） |
| D、（3，8） |
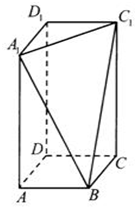在长方体ABCD-A1B1C1D1中，AB=BC=2，过A1，C1，B三点的平面截去长方体的一个角后，得到如图所示的几何体ABCD-A1C1D1，这个几何体的体积为