题目内容
设a＞0，b＞0，则以下不等式中不恒成立的是（ ）
A、（a+b）（
| ||||||
| B、a2+b2+2≥2a+2b | ||||||
| C、a3+a2b≥ab2+b3 | ||||||
D、
|
考点：基本不等式
专题：不等式的解法及应用
分析：对于C利用作差法、不等式的性质即可判断出不恒成立．
解答：
解：对于C：∵a3+a2b-（ab2+b3）
=a2（a+b）-b2（a+b）
=（a+b）（a2-b2）
=（a+b）2（a-b）
又a＞0，b＞0，
∴a-b＞0，或a-b=0或a-b＜0都有可能．
因此a3+a2b≥（ab2+b3）不恒成立．
故选：C．
=a2（a+b）-b2（a+b）
=（a+b）（a2-b2）
=（a+b）2（a-b）
又a＞0，b＞0，
∴a-b＞0，或a-b=0或a-b＜0都有可能．
因此a3+a2b≥（ab2+b3）不恒成立．
故选：C．
点评：本题考查了不等式的性质、作差法，属于基础题．
练习册系列答案
名师指导期末冲刺卷系列答案
开心蛙口算题卡系列答案
相关题目
在△ABC中，已知a=6，b=9，∠A=45°，则这个三角形解的情况是（ ）
| A、有一个解 | B、有两个解 |
| C、无解 | D、不能确定 |
已知函数y=xf′（x）的图象如图所示，则y=f（x）的图象可能是（ ）
A、 |
B、 |
C、 |
D、 |
已知集合A={-1，1，2}，集合B={1，3，5}，则A∩B=（ ）
| A、{-1，1，2，3，5} | B、{1} |
| C、∅ | D、{∅} |
某校五四演讲比赛中，七位评委为一选手打出的分数如下：90，86，90，97，93，94，93，去掉一个最高分和一个最低分后，所剩数据的平均值和方差分别为（ ）
| A、92，2 |
| B、92，2.8 |
| C、93，2 |
| D、93，2.8 |
用数学归纳法证明“5n-2n能被3整除”的第二步中，n=k+1时，为了使用假设，应将5k+1-2k+1变形为（ ）
| A、5（5k-2k）+3×2k |
| B、（5k-2k）+4×5k-2k |
| C、（5-2）（5k-2k） |
| D、2（5k-2k）-3×5k |
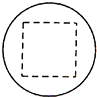已知某一多面体内接于球构成一个简单组合体，如果该组合体的正视图、侧视图、俯视图均如图所示，且图中的四边形是边长为2的正方形，则该球的表面积是（ ）| A、64π | B、32π |
| C、16π | D、12π |
已知双曲线C：
-
=1（a＞0，b＞0）的离心率为
，且过点（
，-2），则C的实轴长为（ ）
| x2 |
| a2 |
| y2 |
| b2 |
| 3 |
| 3 |
| A、2 | ||
| B、2 | ||
C、
| ||
D、2
|