题目内容
已知圆x(x-1)+y(y-1)=0与圆x2+y2=r2(r>
)相内切,则r等于( )
| 1 |
| 2 |
A、
| ||||
| B、1 | ||||
C、
| ||||
D、
|
考点:直线与圆的位置关系
专题:计算题,直线与圆
分析:求出两圆的圆心坐标和半径,利用两圆相内切,两圆的圆心距等于两圆的半径之差解出r,
解答:
解:两圆的圆心坐标分别为(0,0)和(
,
),半径分别为r和
,
两圆相内切,两圆的圆心距等于两圆的半径之差,∴
=r-
,
故r=
.
故选:C.
| 1 |
| 2 |
| 1 |
| 2 |
| ||
| 2 |
两圆相内切,两圆的圆心距等于两圆的半径之差,∴
| ||
| 2 |
| ||
| 2 |
故r=
| 2 |
故选:C.
点评:本题考查圆与圆的位置关系,两圆相内切的充要条件是:两圆的圆心距等于两圆的半径之差,体现了分类讨论的数学思想.

练习册系列答案
相关题目
已知函数y=xf′(x)的图象如图所示,则y=f(x)的图象可能是( )


A、 |
B、 |
C、 |
D、 |
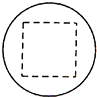 已知某一多面体内接于球构成一个简单组合体,如果该组合体的正视图、侧视图、俯视图均如图所示,且图中的四边形是边长为2的正方形,则该球的表面积是( )
已知某一多面体内接于球构成一个简单组合体,如果该组合体的正视图、侧视图、俯视图均如图所示,且图中的四边形是边长为2的正方形,则该球的表面积是( )| A、64π | B、32π |
| C、16π | D、12π |
已知f(x+1)=
,f(1)=
(x∈N*)猜想f(x)的表达式为( )
| f(x) |
| f(x)+1 |
| 2 |
| 3 |
A、f(x)=
| ||
B、f(x)=
| ||
C、f(x)=
| ||
D、f(x)=
|
若{1,2}⊆A⊆{1,2,3,4,5},则集合A的个数是( )
| A、8 | B、7 | C、4 | D、3 |
如果点P(sinθ,cosθ)位于第三象限,那么角θ所在象限是( )
| A、第一象限 | B、第二象限 |
| C、第三象限 | D、第四象限 |
已知双曲线C:
-
=1(a>0,b>0)的离心率为
,且过点(
,-2),则C的实轴长为( )
| x2 |
| a2 |
| y2 |
| b2 |
| 3 |
| 3 |
| A、2 | ||
| B、2 | ||
C、
| ||
D、2
|