题目内容
3.已知过抛物线方程y2=2px,过焦点F的直线l斜率为k(k>0)与抛物线交于A,B两点,满足$\frac{1}{{|{\overrightarrow{AF}}|}}+\frac{1}{{|{\overrightarrow{FB}}|}}=1$,又$\overrightarrow{AF}=2\overrightarrow{FB}$,则直线l的方程为y=2$\sqrt{2}$(x-1).分析 先求出p的值,再设A,B两点的抛物线的准线上的射影分别为E,F,过B作AE的垂线BC,在三角形ABC中,∠BAC等于直线AB的倾斜角,其正切值即为K值,利用在直角三角形ABC中,求出tan∠BAC,得出直线AB的斜率,即可得出结论.
解答 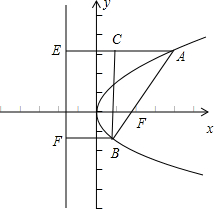 解:∵$\frac{1}{{|{\overrightarrow{AF}}|}}+\frac{1}{{|{\overrightarrow{FB}}|}}=1$,
解:∵$\frac{1}{{|{\overrightarrow{AF}}|}}+\frac{1}{{|{\overrightarrow{FB}}|}}=1$,
∴由抛物线的性质,可得$\frac{2}{p}$=1,∴p=2.
如图,设A,B两点的抛物线的准线上的射影分别为E,F,
过B作AE的垂线BC,
在三角形ABC中,∠BAC等于直线AB的倾斜角,
其正切值即为K值,
设|BF|=n,∵|AF|=2|BF|,∴|AF|=2n,
根据抛物线的定义得:|AE|=2n,|BF|=n,
∴|AC|=n,
在直角三角形ABC中,tan∠BAC=$\frac{BC}{AC}$=2$\sqrt{2}$,
∴直线l的方程为y=2$\sqrt{2}$(x-1).
故答案为y=2$\sqrt{2}$(x-1).
点评 本题主要考查直线与抛物线的位置关系,抛物线的简单性质,特别是焦点弦问题,解题时要善于运用抛物线的定义解决问题.

练习册系列答案
相关题目
11.O为坐标原点,F为抛物线C:y2=4x的焦点,过F的直线交C于A,B且$\overrightarrow{FA}$=2$\overrightarrow{BF}$,则△OAB的面积为( )
| A. | 4 | B. | $\sqrt{2}$ | C. | $\frac{3\sqrt{2}}{2}$ | D. | 2$\sqrt{2}$ |
18.已知袋中装有2个红球和2个白球,随机抽取2个球,则2球都是红球的概率为( )
| A. | $\frac{2}{3}$ | B. | $\frac{1}{6}$ | C. | $\frac{1}{3}$ | D. | $\frac{8}{21}$ |
8.下列说法错误的是( )
| A. | 在△ABC中,若A>B,则cosA<cosB | |
| B. | 若b2=ac,则a,c的等比中项为b | |
| C. | 若命题p与p∧q为真,则q一定为真 | |
| D. | 若p:?x∈(0,+∞),lnx<x-1,则¬p:?x∈(0,+∞),lnx≥x-1 |
13.函数f(x)=x2+2x,x∈[-2,1]的值域为( )
| A. | [-1,3] | B. | [4,8] | C. | [1,3] | D. | [2,3] |