题目内容
11.已知数列{an}满足a1=1,an=a1+$\frac{1}{2}{a_2}+\frac{1}{3}{a_3}+…+\frac{1}{n-1}{a_{n-1}}$(n≥2,n∈N*),若ak=2017,则k=2017.分析 由an=a1+$\frac{1}{2}{a_2}+\frac{1}{3}{a_3}+…+\frac{1}{n-1}{a_{n-1}}$(n≥2,n∈N*),an+1=a1+$\frac{1}{2}{a_2}+\frac{1}{3}{a_3}+…+\frac{1}{n-1}{a_{n-1}}$+$\frac{1}{n}$an,(n≥2,n∈N*),两式相减整理得:$\frac{{a}_{n+1}}{{a}_{n}}$=$\frac{n+1}{n}$,累乘即可求得an=n,即可求得k的值.
解答 解:根据题意得,an=a1+$\frac{1}{2}{a_2}+\frac{1}{3}{a_3}+…+\frac{1}{n-1}{a_{n-1}}$(n≥2,n∈N*),
an+1=a1+$\frac{1}{2}{a_2}+\frac{1}{3}{a_3}+…+\frac{1}{n-1}{a_{n-1}}$+$\frac{1}{n}$an,(n≥2,n∈N*),
∴an+1=an+$\frac{1}{n}$an,
∴$\frac{{a}_{n+1}}{{a}_{n}}$=$\frac{n+1}{n}$,
an=2×$\frac{3}{2}$×…×$\frac{n}{n-1}$=n,(n≥2,n∈N*),
∴an=n,
由ak=2017,则k=2017,
故答案为:2017.
点评 本题考查数列的递推公式,考查数列通项公式的求法,考查计算能力,属于中档题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
1.已知f(x)是R上的可导函数,其导函数为f'(x),若对任意实数x,都有f(x)>f'(x),且f(x)-1为奇函数,则不等式f(x)<ex的解集为( )
| A. | (-∞,0) | B. | (-∞,e4) | C. | (e4,+∞) | D. | (0,+∞) |
2.点M的直角坐标是$(-\sqrt{3},-1)$,则点M的极坐标为( )
| A. | $(2,\frac{5π}{6})$ | B. | $(2,\frac{7π}{6})$ | C. | $(2,\frac{11π}{6})$ | D. | $(2,\frac{π}{6})$ |
3.总体由编号为01,02,03,…,49,50的50个个体组成,利用随机数表(以下选取了随机数表中的第1行和第2行)选取5个个体,选取方法是从随机数表第1行的第9列和第10列数字开始由左向右读取,则选出来的第4个个体的编号为( )
| 78 16 65 72 08 02 63 14 07 02 43 69 69 38 74 |
| 32 04 94 23 49 55 80 20 36 35 48 69 97 28 01 |
| A. | 05 | B. | 09 | C. | 07 | D. | 20 |
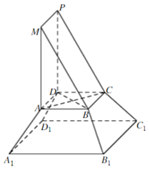 《九章算术》是我国古代内容极为丰富的数学名著,书中将底面为直角三角形,且侧棱与底面垂直的棱柱称为堑堵,将底面为矩形的棱台称为刍童.在如图所示的堑堵ABM-DCP与刍童的组合体中AB=AD,A1B1=A1D1.棱台体积公式:V=$\frac{1}{3}$(S′+$\sqrt{S′S}$+S)h,其中S′,S分别为棱台上、下底面面积,h为棱台高.
《九章算术》是我国古代内容极为丰富的数学名著,书中将底面为直角三角形,且侧棱与底面垂直的棱柱称为堑堵,将底面为矩形的棱台称为刍童.在如图所示的堑堵ABM-DCP与刍童的组合体中AB=AD,A1B1=A1D1.棱台体积公式:V=$\frac{1}{3}$(S′+$\sqrt{S′S}$+S)h,其中S′,S分别为棱台上、下底面面积,h为棱台高.