题目内容
6.(1)已知$sinα=\frac{3}{5}$,$cosβ=\frac{4}{5}$,其中$α∈(\frac{π}{2},π)$,$β∈(0,\frac{π}{2})$,求cos(α+β);(2)已知$cosα=\frac{1}{7}$,$cos(α-β)=\frac{13}{14}$,且$0<β<α<\frac{π}{2}$,求β的值.
分析 (1)由已知利用同角三角函数基本关系式可求$cosα=-\frac{4}{5}$,$sinβ=\frac{3}{5}$,利用两角和的余弦函数公式即可计算得解.
(2)由已知利用同角三角函数基本关系式可求sinα,sin(α-β)的值,进而利用两角差的正弦函数公式即可计算得解sinβ的值,结合范围可求β的值.
解答 解:(1)∵$α∈(\frac{π}{2},π)$,$β∈(0,\frac{π}{2})$,$sinα=\frac{3}{5}$,$cosβ=\frac{4}{5}$,
∴$cosα=-\frac{4}{5}$,$sinβ=\frac{3}{5}$,
∴cos(α+β)=cosαcosβ-sinαsinβ=$(-\frac{4}{5})×\frac{4}{5}-\frac{3}{5}×\frac{3}{5}=-1$.
(2)∵$0<α<\frac{π}{2}$,$cosα=\frac{1}{7}$,∴$sinα=\frac{{4\sqrt{3}}}{7}$,
∵$0<β<α<\frac{π}{2}$,$cos(α-β)=\frac{13}{14}$,∴$0<α-β<\frac{π}{2}$,∴$sin(α-β)=\frac{{3\sqrt{3}}}{14}$,
∴sinβ=sin(α-(α-β))=sinαcos(α-β)-cosαsin(α-β)=$\frac{{4\sqrt{3}}}{7}×\frac{13}{14}-\frac{1}{7}×\frac{{3\sqrt{3}}}{14}=\frac{{\sqrt{3}}}{2}$,
∴$β=\frac{π}{3}$.
点评 本题主要考查了同角三角函数基本关系式,两角和的余弦函数公式,两角差的正弦函数公式在三角函数化简求值中的应用,考查了转化思想,属于基础题.

 小学学习好帮手系列答案
小学学习好帮手系列答案 小学同步三练核心密卷系列答案
小学同步三练核心密卷系列答案| A. | 5 | B. | 6 | C. | 7 | D. | 8 |
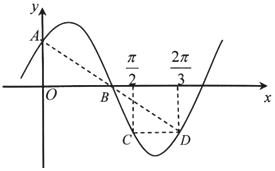 如图,已知函数f(x)=sin(ωx+φ)(ω>0,0<φ<π),点A,B分别是f(x)的图象与y轴、x轴的交点,C,D分别是f(x)的图象上横坐标为$\frac{π}{2}$、$\frac{2π}{3}$的两点,CD∥x轴,A,B,D共线.
如图,已知函数f(x)=sin(ωx+φ)(ω>0,0<φ<π),点A,B分别是f(x)的图象与y轴、x轴的交点,C,D分别是f(x)的图象上横坐标为$\frac{π}{2}$、$\frac{2π}{3}$的两点,CD∥x轴,A,B,D共线.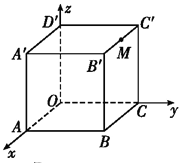 如图,棱长为2的正方体OABC-D′A′B′C′中,点M在B′C′上,且M为B′C′的中点,若以O为坐标原点,建立空间直角坐标系,则点M的坐标为(1,2,2).
如图,棱长为2的正方体OABC-D′A′B′C′中,点M在B′C′上,且M为B′C′的中点,若以O为坐标原点,建立空间直角坐标系,则点M的坐标为(1,2,2).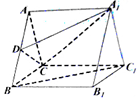 如图,在直三棱柱ABC-A1B1C1中,底面△ABC是边长为2的等边三角形,D为AB的中点.
如图,在直三棱柱ABC-A1B1C1中,底面△ABC是边长为2的等边三角形,D为AB的中点.