题目内容
在上学期的期末考试中A、B、C、D四位同学的名次分别为1，2，3，4名，求这次期中考试中：
（1）B同学考第一的概率；
（2）仅有两人名次改变的概率．
（1）B同学考第一的概率；
（2）仅有两人名次改变的概率．
考点：互斥事件的概率加法公式,相互独立事件的概率乘法公式
专题：概率与统计
分析：（1）根据相互独立事件求解；
（2）是古典概型，先找出事件的所有可能发生的情况，再找出次事件发生的情况，从而求解．
（2）是古典概型，先找出事件的所有可能发生的情况，再找出次事件发生的情况，从而求解．
解答：
解：（1）因为在这次期中考试中，谁取得第一相互独立，故B同学考第一的概率是
；
（2）在这次期中考试中，共有A44=24中排名，而仅有两人名次改变的有C42A22=12种，
故仅有两人名次改变的概率是：
=
．
| 1 |
| 4 |
（2）在这次期中考试中，共有A44=24中排名，而仅有两人名次改变的有C42A22=12种，
故仅有两人名次改变的概率是：
| 12 |
| 24 |
| 1 |
| 2 |
点评：本题主要考查相互独立事件的概率的求法和古典概率，属于基础题．
练习册系列答案
开心蛙状元测试卷系列答案
相关题目
设U=R，A={x|x＞0}，B={x|x＞1}，则A∪B=（ ）
| A、{x|0≤x＜1} |
| B、{x|0＜x≤1} |
| C、{x|x＞0} |
| D、{x|x＞1} |
cos420°的值为（ ）
A、
| ||||
B、-
| ||||
C、
| ||||
D、-
|
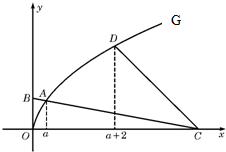如图，曲线G的方程为y=
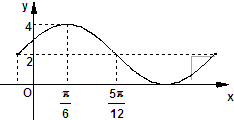已知函数f（x）=Asin（ωx+ϕ）+B的一部分图象如图所示，如果A＞0，ω＞0，|φ|＜