题目内容
已知命题p：?x∈（-∞，0），2x＜3x，命题q：?x∈（0，1），log2x＜0，则下列命题为真命题的是（ ）
| A、p∧q |
| B、p∨（﹁q） |
| C、（﹁p）∧q |
| D、p∧（﹁q） |
考点：复合命题的真假
专题：计算题,简易逻辑
分析：先根据指数函数的单调性判定出命题p为假命题，再根据对数函数的单调性判定出命题q为真命题，根据复合命题的真值表得出￢p∧q为真命题
解答：
解：因为y=
=(
)x为增函数
当x=0时y=1
所以对?x∈（-∞，0），y=
=(
)x＜1
所以2x＞3x
所以命题p为假命题
所以￢p为真命题
因为函数y=log2x为增函数，
又log21=0
所以对?x∈（0，1），log2x＜0
所以命题q为真命题
所以￢p∧q为真命题
故选C
| 3x |
| 2x |
| 3 |
| 2 |
当x=0时y=1
所以对?x∈（-∞，0），y=
| 3x |
| 2x |
| 3 |
| 2 |
所以2x＞3x
所以命题p为假命题
所以￢p为真命题
因为函数y=log2x为增函数，
又log21=0
所以对?x∈（0，1），log2x＜0
所以命题q为真命题
所以￢p∧q为真命题
故选C
点评：本题考查的知识点是复合命题的真假判定，属于基础题目
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
已知复数z=a+bi（a，b∈R），且|z-2|=
，则a、b满足的轨迹方程是（ ）
| 5 |
| A、（a-2）2+b2=5 |
| B、（a+2）2+b2=5 |
| C、a2+（b-2）2=5 |
| D、a2+（b+2）2=5 |
设a＞0，b＞0，e是自然对数的底数，则（ ）
| A、若ea-3b=eb-2a，则a＜b |
| B、若ea-3b=eb-2a，则a＞b |
| C、若ea+3b=eb+2a，则a＜b |
| D、若ea+3b=eb+2a，则a＞b |
已知函数y=f（x）的导函数存在，则函数y=f（x）在一点的导数值为0是函数y=f（x）在这点取极值的（ ）
| A、充分不必要条件 |
| B、必要不充分条件 |
| C、充要条件 |
| D、既不充分也不必要条件 |
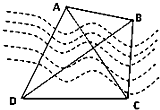如图，A、B两点都在河的对岸（不可到达），为了测量A、B两点间的距离，选取一条基线CD，A、B、C、D在一平面内．测得：CD=200m，∠ADB=∠ACB=30°，∠CBD=60°，则AB=（ ）A、
| ||||
B、200
| ||||
C、100
| ||||
| D、数据不够，无法计算 |
α为平面，m，n是两条不同直线，则m∥n的一个充分条件是（ ）
| A、m∥α且n∥α |
| B、m，n与平面α所成的角相等 |
| C、m⊥α且n⊥α |
| D、m，n与平面α的距离相等 |
若集合A={x|0≤x＜1}，B={x|x2＜2x}，则A∩B=（ ）
| A、{x|0＜x＜1} |
| B、{x|0≤x＜1} |
| C、{x|0＜x≤1} |
| D、{x|0≤x≤1} |