题目内容
已知梯形ABCD中,AD∥BC,∠ABC=∠BAD=
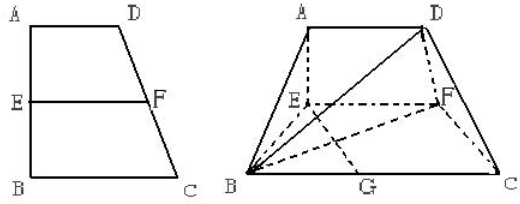
,G是BC的中点.AB=BC=2AD=4,E、F分别是AB、CD上的动点,且EF∥BC,设AE=x(0<x<2),沿EF将梯形ABCD翻折,使使平面AEFD⊥平面EBCF,如图.
(1)当x=2时,求证:BD⊥EG;
(2)若以B、C、D、F为顶点的三棱锥的体积记为f(x),求f(x)的最大值;
(3)当f(x)取得最大值时,求二面角D-BF-C的余弦值.
| π |
| 2 |
(1)当x=2时,求证:BD⊥EG;
(2)若以B、C、D、F为顶点的三棱锥的体积记为f(x),求f(x)的最大值;
(3)当f(x)取得最大值时,求二面角D-BF-C的余弦值.

考点:棱柱、棱锥、棱台的体积,二面角的平面角及求法
专题:空间位置关系与距离,空间角,空间向量及应用
分析:(1)利用面面垂直的性质证线面垂直,由线面垂直⇒线线垂直,再由线线垂直证线面垂直,由线面垂直的性质证得线线垂直;
(2)根据题意先求得棱锥的高,再根据体积公式求三棱锥的体积即可.
(3)可利用空间向量求解.根据条件可得AE⊥EF,AE⊥BE,BE⊥EF故可建立如图所示的空间直角坐标系然后求出面DBF和面EBF的法向量则两个法向量的夹角即为二面角的平面角然后利用向量夹角公式即可求出二面角D-BF-E的余弦值.
(2)根据题意先求得棱锥的高,再根据体积公式求三棱锥的体积即可.
(3)可利用空间向量求解.根据条件可得AE⊥EF,AE⊥BE,BE⊥EF故可建立如图所示的空间直角坐标系然后求出面DBF和面EBF的法向量则两个法向量的夹角即为二面角的平面角然后利用向量夹角公式即可求出二面角D-BF-E的余弦值.
解答:
(1)证明:作DH⊥EF,垂足H,连结BH,GH,
∵平面AEFD⊥平面EBCF,交线EF,DH?平面AEFD,
∴DH⊥平面EBCF,又EG?平面EBCF,故EG⊥DH.
∵EH=AD=
BC=BG,EF∥BC,∠ABC=90°.
∴四边形BGHE为正方形,∴EG⊥BH.
又BH、DH?平面DBH,且BH∩DH=H,故EG⊥平面DBH.
又BD?平面DBH,∴EG⊥BD.
(2)∵AE⊥EF,平面AEFD⊥平面EBCF,交线EF,AE?平面AEFD.
∴AE⊥面EBCF.又由(1)DH⊥平面EBCF,故AE∥GH,
∴四边形AEHD是矩形,DH=AE,故以F、B、C、D为顶点的三
棱锥D-BCF的高DH=AE=x.
又S△BCF=
×BC•BE=
×4×(4-x)=8-2x,(0≤x≤4).
∴三棱锥D-BCF的体积f(x)=
×S△BFC•DH=
×S△BFC×AE=
×(8-2x)•x=
-
,(0≤x≤4).
(3)f(x)═
-
,(0≤x≤4).
当x=2时,f(x)取最大值
,
(2)∵AE⊥面平面EBCF,AE⊥EF,AE⊥BE,又BE⊥EF,
故可如图建立空间坐标系E-xyz
则A(0,0,2),B(2,0,0),G(2,2,0),D(0,2,2),E(0,0,0)
设平面DBF的法向量为
=(x,y,z)
∵AE=2,B(2,0,0),D(0,2,2),F(0,3,0)
∴
=(-2,3,0),
=(-2,2,2)
则
即
取x=3,则y=2,z=1
∴
=(3,2,1)
平面BCF的一个法向量为
=(0,0,1)
记此二面角的平面角为θ,则
=
=
,
∵二面角D-BF-C是钝二面角
∴此二面角的余弦值为cosθ=-
∵平面AEFD⊥平面EBCF,交线EF,DH?平面AEFD,
∴DH⊥平面EBCF,又EG?平面EBCF,故EG⊥DH.
∵EH=AD=
| 1 |
| 2 |
∴四边形BGHE为正方形,∴EG⊥BH.
又BH、DH?平面DBH,且BH∩DH=H,故EG⊥平面DBH.

又BD?平面DBH,∴EG⊥BD.
(2)∵AE⊥EF,平面AEFD⊥平面EBCF,交线EF,AE?平面AEFD.
∴AE⊥面EBCF.又由(1)DH⊥平面EBCF,故AE∥GH,
∴四边形AEHD是矩形,DH=AE,故以F、B、C、D为顶点的三
棱锥D-BCF的高DH=AE=x.
又S△BCF=
| 1 |
| 2 |
| 1 |
| 2 |
∴三棱锥D-BCF的体积f(x)=
| 1 |
| 3 |
| 1 |
| 3 |
| 1 |
| 3 |
| 8x |
| 3 |
| 2x2 |
| 3 |
(3)f(x)═
| 8x |
| 3 |
| 2x2 |
| 3 |
当x=2时,f(x)取最大值
| 8 |
| 3 |
(2)∵AE⊥面平面EBCF,AE⊥EF,AE⊥BE,又BE⊥EF,
故可如图建立空间坐标系E-xyz
则A(0,0,2),B(2,0,0),G(2,2,0),D(0,2,2),E(0,0,0)
设平面DBF的法向量为
| n1 |
∵AE=2,B(2,0,0),D(0,2,2),F(0,3,0)
∴
| BF |
| BD |
则
|
即
|
取x=3,则y=2,z=1
∴
| n1 |

平面BCF的一个法向量为
| n2 |
记此二面角的平面角为θ,则
| ||||
|
|
| 1 | ||
|
| ||
| 14 |
∵二面角D-BF-C是钝二面角
∴此二面角的余弦值为cosθ=-
| ||
| 14 |
点评:本题主要考察了三棱锥体积和二面角的求解.解题的关键是在求三棱锥体积时主要是高的求解这要充分分析题中条件找到高或‘等价的高'而对于二面角的求解可采用空间向量的方法即求出二面角的两个半平面的法向量然后利用向量的夹角公式求出法向量的夹角的余弦值再结合图形特征和法向量的夹角的余弦值的正负得出二面角的大小是法向量的夹角还是其补角,但此法计算量较大,因此在以后的学习中要加强计算能力的训练!

练习册系列答案
 手拉手全优练考卷系列答案
手拉手全优练考卷系列答案
相关题目
在同一坐标系中,函数y=3x的图与y=(
)x的图象( )
| 1 |
| 3 |
| A、关于x轴对称 |
| B、关于y轴对称 |
| C、关于原点对称 |
| D、关于直线y=x对称 |
若A为抛物线y=
x2的顶点,过抛物线焦点的直线交抛物线于B、C两点,则
•
等于( )
| 1 |
| 4 |
| AB |
| AC |
| A、-3 | B、3 | C、5 | D、-5 |
命题“?x∈[-2,1],x2-a≤0”为真命题的一个必要不充分条件是( )
| A、a≥4 | B、a≥1 |
| C、a≤4 | D、a≤1 |
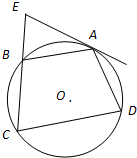 如图,四边形ABCD的外接圆为⊙O,EA是⊙O的切线,CB的延长线与EA相交于点E,AB=AD.求证:AB2=BE•CD.
如图,四边形ABCD的外接圆为⊙O,EA是⊙O的切线,CB的延长线与EA相交于点E,AB=AD.求证:AB2=BE•CD.