题目内容
设数列{an}满足:a1=5,an+1+4an=5
(Ⅰ)求证:{an-1}是等比数列;
(Ⅱ)设数列bn=|an|,求|bn|的前2014项和S2014.
(Ⅰ)求证:{an-1}是等比数列;
(Ⅱ)设数列bn=|an|,求|bn|的前2014项和S2014.
考点:数列的求和,等比关系的确定
专题:等差数列与等比数列
分析:(Ⅰ)根据等比数列的定义即可证明{an-1}是等比数列;
(Ⅱ)求出数列bn=|an|的通项公式,利用分组求和法即可求|bn|的前2014项和S2014.
(Ⅱ)求出数列bn=|an|的通项公式,利用分组求和法即可求|bn|的前2014项和S2014.
解答:
解:(Ⅰ)∵a1=5,an+1+4an=5,
∴an+1=5-4an,
即an+1-1=-4(an-1),
∵a1-1=5-1=4,
∴{an-1}是公比q=-4,首项为4的等比数列;
(Ⅱ)∵{an-1}是公比q=-4,首项为4的等比数列;
∴an-1=4•(-4)n-1,即an=4•(-4)n-1+1.
若n为奇数,则bn=|an|=|4•(-4)n-1+1|=1+4n,
若n为偶数,则bn=|an|=|4•(-4)n-1+1|=4n-1.
则|bn|的前2014项和S2014=(1+4)+(42-1)+(1+43)+…+(1-42013)+(42014-1)
=1+4+42+43+…+42013+42014=
=
.
∴an+1=5-4an,
即an+1-1=-4(an-1),
∵a1-1=5-1=4,
∴{an-1}是公比q=-4,首项为4的等比数列;
(Ⅱ)∵{an-1}是公比q=-4,首项为4的等比数列;
∴an-1=4•(-4)n-1,即an=4•(-4)n-1+1.
若n为奇数,则bn=|an|=|4•(-4)n-1+1|=1+4n,
若n为偶数,则bn=|an|=|4•(-4)n-1+1|=4n-1.
则|bn|的前2014项和S2014=(1+4)+(42-1)+(1+43)+…+(1-42013)+(42014-1)
=1+4+42+43+…+42013+42014=
| 1-42015 |
| 1-4 |
| 42015-1 |
| 3 |
点评:本题主要考查等比数列的通项公式以及前n项和的计算,考查学生的运算能力.

练习册系列答案
 小学生10分钟口算测试100分系列答案
小学生10分钟口算测试100分系列答案
相关题目
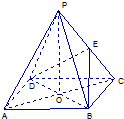 如图所示,ABCD是正方形,O是正方形的中心,PO⊥底面ABCD,底面边长AB=1,E是PC的中点.
如图所示,ABCD是正方形,O是正方形的中心,PO⊥底面ABCD,底面边长AB=1,E是PC的中点.