题目内容
10.已知(1-x)6=a0+a1x+a2x2+…+a6x6,则|a0|+|a1|+…+|a6|=64.分析 根据二项式定理可知a0,a2,a4,a6均为正数,a1,a3,a5均为负数,令x=-1即可求出结论.
解答 解:${(1-x)^6}={a_0}+{a_1}x+{a_2}{x^2}+…+{a_6}{x^6}$,
由二项式定理可知a0,a2,a4,a6均为正数,a1,a3,a5均为负数,
∴令x=-1,得(1+1)6=a0-a1+a2-…+a6=26=64,
即|a0|+|a1|+…+|a6|=a0-a1+a2-…+a6=64.
故答案为:64.
点评 本题考查了用赋值法求二项式展开式的各项系数和的应用问题,是基础题目.

练习册系列答案
 一本好题口算题卡系列答案
一本好题口算题卡系列答案
相关题目
20.i为虚数单位,则复数$\frac{1-2i}{i}$的共轭复数是( )
| A. | -1+2i | B. | 1-2i | C. | -2+i | D. | 2-i |
1.等差数列{an}中,a2=5,a4=9,则{an}的前5项和S5=( )
| A. | 14 | B. | 25 | C. | 35 | D. | 40 |
2.阅读如图的程序框图,运行相应的程序,则输出S的值为( )


| A. | 10 | B. | 13 | C. | -10 | D. | -13 |
19.设集合A={x|x2-x-6<0,x∈R},B={y|y=|x|-3,x∈A},则A∩B等于( )
| A. | {x|0<x<3} | B. | {x|-1<x<0} | C. | {x|-2<x<0} | D. | {x|-3<x<3} |
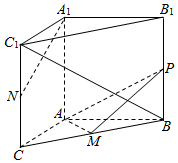 如图,在三棱柱ABC-A1B1C1中,AA1⊥底面ABC,∠BAC=90°,AB=AC=2,$A{A_1}=\sqrt{3}$.M,N分别为BC和CC1的中点,P为侧棱BB1上的动点.
如图,在三棱柱ABC-A1B1C1中,AA1⊥底面ABC,∠BAC=90°,AB=AC=2,$A{A_1}=\sqrt{3}$.M,N分别为BC和CC1的中点,P为侧棱BB1上的动点.