题目内容
16.直线y=2x+b是曲线y=xlnx(x>0)的一条切线,则实数b为-e.分析 设切点为(x0,x0lnx0),对y=xlnx求导数得y′=lnx+1,从而得到切线的斜率k=lnx0+1,结合直线方程的点斜式化简得切线方程为y=(lnx0+1)x-x0,对照已知直线列出关于x0、m的方程组,解之即可得到实数m的值.
解答 解:设切点为(x0,x0lnx0),
对y=xlnx求导数,得y′=lnx+1,
∴切线的斜率k=lnx0+1,
故切线方程为y-x0lnx0=(lnx0+1)(x-x0),
整理得y=(lnx0+1)x-x0,
与y=2x+b比较得lnx0+1=2且-x0=b,
解得x0=e,故b=-e.
故b的值为:-e.
点评 本题考查导数的几何意义,切线方程的求法,考查计算能力,属于中档题.

练习册系列答案
相关题目
15.银川一中在高一、高二两个年级学生中各抽取100人的样本,进行普法知识调查,其结果如表:
(1)求x,y的值.
(2)在犯错误的概率不超过1%的情况下,是否认为“高一、高二两个年级这次普法知识调查结果有差异”?
参考公式:K2=$\frac{n(ad-bc)^{2}}{(a+b)(c+d)(a+c)(b+d)}$
| 高一 | 高二 | 总计 | |
| 合格人数 | 70 | x | 150 |
| 不合格人数 | y | 20 | 50 |
| 总计 | 100 | 100 | 200 |
(2)在犯错误的概率不超过1%的情况下,是否认为“高一、高二两个年级这次普法知识调查结果有差异”?
参考公式:K2=$\frac{n(ad-bc)^{2}}{(a+b)(c+d)(a+c)(b+d)}$
| P(K2≥k0) | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| k0 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
1.椭圆$\frac{x^2}{9}+\frac{y^2}{2}=1$的焦点为F1,F2,点P在椭圆上,若|PF1|=2,则∠F1PF2=( )
| A. | 30o | B. | 60o | C. | 120o | D. | 150o |
8.在△ABC中,A=30°,则$\sqrt{3}sinA-cos({B+C})$的值为( )
| A. | $\sqrt{2}$ | B. | $\sqrt{3}$ | C. | $\frac{{\sqrt{3}}}{2}$ | D. | 2 |
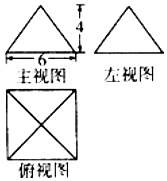 已知某几何体的三视图如图所示,俯视图是正方形,正视图和侧视图都是底面边长为6,高为4的等腰三角形.
已知某几何体的三视图如图所示,俯视图是正方形,正视图和侧视图都是底面边长为6,高为4的等腰三角形.