题目内容
11.在△ABC中,BC=20,tanB•tanC=$\frac{1}{4}$,AC=4$\sqrt{2}$,则cosA=$-\frac{3\sqrt{34}}{34}$.分析 过A作BC的高交BC于H,高为h,CH设为x,tanC=$\frac{h}{x}$,tanB=$\frac{h}{20-x}$,可得:$\frac{h}{x}•\frac{h}{20-x}=\frac{1}{4}$,${h}^{2}+{x}^{2}=(4\sqrt{2})^{2}$求出h和x.确定C的大小.利用余弦定理求解AB,在求cosA的值.
解答 解:由BC=a=20,AC=b=4$\sqrt{2}$,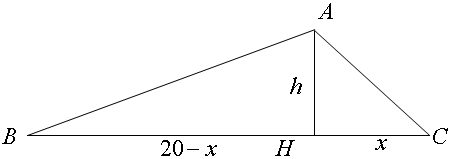
过A作BC的高交BC于H,高为h,CH设为x
tanC=$\frac{h}{x}$,
tanB=$\frac{h}{20-x}$
可得:$\frac{h}{x}•\frac{h}{20-x}=\frac{1}{4}$
${h}^{2}+{x}^{2}=(4\sqrt{2})^{2}$
解得:x=h=4.
∴C=45°.
由余弦定理cosC=$\frac{{a}^{2}+{b}^{2}-{c}^{2}}{2ab}$,
可得:$\frac{\sqrt{2}}{2}$×$2×20×4\sqrt{2}$=400+32-c2.
解得:c=4$\sqrt{17}$.
那么:cosA=$\frac{{c}^{2}+{b}^{2}-{a}^{2}}{2bc}$=$-\frac{3\sqrt{34}}{34}$.
故答案为:$-\frac{3\sqrt{34}}{34}$.
点评 本题考查三角形的正余弦定理和内角和定理的运用,考查运算能力,属于中档题.

练习册系列答案
 寒假乐园北京教育出版社系列答案
寒假乐园北京教育出版社系列答案
相关题目
10.复数(i-$\frac{1}{i}$)3的虚部是( )
| A. | -8 | B. | -8i | C. | 8 | D. | 8i |
2.用数学归纳法证明1+2+3+4+…++(2n-1)+2n=2n2+n,当n=k+1时左端应在n=k时的基础上加的项是( )
| A. | 2k+1 | B. | 2k+2 | C. | (2k+1)+(2k+2) | D. | 1 |
1.已知四面体P-ABC的外接球的球心O在AB上,且PO⊥平面ABC,2AC=$\sqrt{3}$AB,若四面体P-ABC 的体积为$\frac{3}{2}$,求球的表面积( )
| A. | 8π | B. | 12π | C. | 8$\sqrt{3}$π | D. | 12$\sqrt{3}$π |