题目内容
11.偶函数f(x)=Asin(ωx+φ)(A≠0,ω>0,0≤φ≤π)的图象向右平移$\frac{π}{4}$个单位得到的图象关于原点对称,则ω的值可以为( )| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
分析 先由条件利用正弦函数、余弦函数的奇偶性求得φ=$\frac{π}{2}$,f(x)=Acosωx,再根据y=Asin(ωx+φ)的图象变换规律以及正弦函数、余弦函数的奇偶性,结合所给的选项求得ω 的值.
解答 解:∵偶函数f(x)=Asin(ωx+φ)(A≠0,ω>0,0≤φ≤π),
∴φ=$\frac{π}{2}$,f(x)=Asin(ωx+$\frac{π}{2}$)=Acosωx,
把它的图象向右平移$\frac{π}{4}$个单位得到y=Acosω(x-$\frac{π}{4}$)=Acos(ωx-ω•$\frac{π}{4}$)的图象,
再根据所得图象关于原点对称,则ω 可以等于2,
故选:B.
点评 本题主要考查诱导公式,y=Asin(ωx+φ)的图象变换规律,正弦函数、余弦函数的奇偶性,属于基础题.

练习册系列答案
相关题目
1.函数f(x)=$\frac{lg(x+2)}{x-1}$的定义域是( )
| A. | (-2,1) | B. | [-2,1)∪(1,+∞) | C. | (-2,+∞) | D. | (-2,1)∪(1,+∞) |
16.i是虚数单位,复数2i=z(-1+i),则z的共轭复数是( )
| A. | -1+i | B. | -i+1 | C. | i+1 | D. | -i-1 |
3.已知圆锥的母线长是10,侧面展开图是半圆,则该圆锥的侧面积为( )
| A. | $\frac{100}{3}$π | B. | 100π | C. | $\frac{50}{3}$π | D. | 50π |
1.从装有3个红球和2个黑球的口袋内任取2个球,那么对立的两个事件是( )
| A. | 至少有1个黑球与都是红球 | B. | 至少有1个黑球与都是黑球 | ||
| C. | 至少有1个黑球与至少有1个红球 | D. | 恰有1个黑球与恰有2个黑球 |
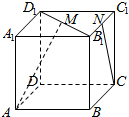 正方体ABCD-A1B1C1D1的棱长为2,点M和N分别是B1D1和B1C1的中点,则异面直线AM和CN所成角的余弦值为$\frac{\sqrt{30}}{10}$.
正方体ABCD-A1B1C1D1的棱长为2,点M和N分别是B1D1和B1C1的中点,则异面直线AM和CN所成角的余弦值为$\frac{\sqrt{30}}{10}$.