题目内容
16.已知函数f(x)=$\sqrt{|x+5|-|x-1|+t}$的定义域为R.(1)求实数t的取值范围;
(2)若t的最小值为s,正实数a、b满足$\frac{2}{a+2b}$+$\frac{1}{2a+b}$=s,求4a+5b的最小值.
分析 (1)求出函数y=|x+5|-|x-1|的值域为[-6,6],由恒成立可得t≥6;
(2)换元法:令a+2b=m,2a+b=n,问题转化为正数m,n满足$\frac{2}{m}$+$\frac{1}{n}$=6,求2m+n的最小值问题,由基本不等式可得.
解答 解:(1)研究函数y=|x+5|-|x-1|,
当x≤-5时,y=-6,当x≥1时,y=6,
当-5<x<1时,y=2x+4∈(-6,6),
故函数y=|x+5|-|x-1|的值域为[-6,6],
∵函数f(x)=$\sqrt{|x+5|-|x-1|+t}$的定义域为R,
∴被开方的式子恒大于等于0,故t≥6;
(2)由(1)知正实数a、b满足$\frac{2}{a+2b}$+$\frac{1}{2a+b}$=6,
令a+2b=m,2a+b=n,则正数m,n满足$\frac{2}{m}$+$\frac{1}{n}$=6,
则4a+5b=2m+n=$\frac{1}{6}$(2m+n)($\frac{2}{m}$+$\frac{1}{n}$)
=$\frac{1}{6}$(5+$\frac{2n}{m}$+$\frac{2m}{n}$)≥$\frac{1}{6}$(5+2$\sqrt{\frac{2n}{m}•\frac{2m}{n}}$)=$\frac{3}{2}$
当且仅当$\frac{2n}{m}$=$\frac{2m}{n}$即m=n=$\frac{1}{2}$时取等号,此时a=b=$\frac{1}{6}$,
故4a+5b的最小值为$\frac{3}{2}$
点评 本题考查基本不等式求最值,涉及函数恒成立和换元的思想,属中档题.

练习册系列答案
 口算题卡加应用题集训系列答案
口算题卡加应用题集训系列答案 综合自测系列答案
综合自测系列答案
相关题目
7.已知[t]表示不超过t的最大整数,例如[1.25]=1,[2]=2,若关于x的方程$\frac{[x]}{x-1}$=a在(1,+∞)恰有2个不同的实数解,则实数a的取值范围是( )
| A. | [2,+∞) | B. | (2,+∞) | C. | ($\frac{3}{2}$,2] | D. | [$\frac{3}{2}$,2] |
1.从装有3个红球和2个黑球的口袋内任取2个球,那么对立的两个事件是( )
| A. | 至少有1个黑球与都是红球 | B. | 至少有1个黑球与都是黑球 | ||
| C. | 至少有1个黑球与至少有1个红球 | D. | 恰有1个黑球与恰有2个黑球 |
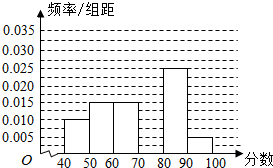 某校从参加高一年级期中考试的学生中随机抽出60名学生,将其物理成绩(均为整数)分成六段[40,50)、[50,60)、…、[90,100)后得到如图所示的频率分布直方图.观察图形的信息,回答下列问题:
某校从参加高一年级期中考试的学生中随机抽出60名学生,将其物理成绩(均为整数)分成六段[40,50)、[50,60)、…、[90,100)后得到如图所示的频率分布直方图.观察图形的信息,回答下列问题: