题目内容
14.函数f(x)=ax-1-2(a>0,a≠1)的图象恒过定点A,若点A在直线mx-ny-1=0上,其中m>0,n>0,则$\frac{1}{m}+\frac{2}{n}$的最小值为( )| A. | 4 | B. | 5 | C. | 6 | D. | $3+2\sqrt{2}$ |
分析 由指数函数可得A坐标,可得m+n=1,整体代入可得$\frac{1}{m}+\frac{2}{n}$=($\frac{1}{m}+\frac{2}{n}$)(m+n)=3+$\frac{n}{m}$+$\frac{2m}{n}$,由基本不等式可得.
解答 解:当x-1=0即x=1时,ax-1-2恒等于-1,
故函数f(x)=ax-1-2(a>0,a≠1)的图象恒过定点A(1,-1),
由点A在直线mx-ny-1=0上可得m+n=1,
由m>0,n>0可得$\frac{1}{m}+\frac{2}{n}$=($\frac{1}{m}+\frac{2}{n}$)(m+n)
=3+$\frac{n}{m}$+$\frac{2m}{n}$≥3+2$\sqrt{\frac{n}{m}•\frac{2m}{n}}$=3+2$\sqrt{2}$
当且仅当$\frac{n}{m}$=$\frac{2m}{n}$即m=$\sqrt{2}$-1且n=2-$\sqrt{2}$时取等号,
故选:D.
点评 本题考查基本不等式求最值,涉及指数函数的性质,属基础题.

练习册系列答案
相关题目
4.下列各式中正确的是( )
| A. | -$\sqrt{x}$=(-x)${\;}^{\frac{1}{2}}$ | B. | x${\;}^{-\frac{1}{5}}$=-$\root{5}{x}$ | C. | (-x)${\;}^{\frac{2}{3}}$=x${\;}^{\frac{2}{3}}$ | D. | x${\;}^{\frac{2}{6}}$=x${\;}^{\frac{1}{3}}$ |
9.已知四面体ABCD,$\overrightarrow{DA}$=$\overrightarrow{a}$,$\overrightarrow{DB}$=$\overrightarrow{b}$,$\overrightarrow{DC}$=$\overrightarrow{c}$,点M在棱DA上,$\overrightarrow{DM}$=2$\overrightarrow{MA}$,N为BC中点,则$\overrightarrow{MN}$=( )
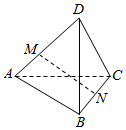

| A. | -$\frac{2}{3}$$\overrightarrow{a}$-$\frac{1}{2}$$\overrightarrow{b}$-$\frac{1}{2}$$\overrightarrow{c}$ | B. | -$\frac{2}{3}$$\overrightarrow{a}$+$\frac{1}{2}$$\overrightarrow{b}$+$\frac{1}{2}$$\overrightarrow{c}$ | C. | $\frac{2}{3}$$\overrightarrow{a}$+$\frac{1}{2}$$\overrightarrow{b}$+$\frac{1}{2}$$\overrightarrow{c}$ | D. | $\frac{2}{3}$$\overrightarrow{a}$-$\frac{1}{2}$$\overrightarrow{b}$-$\frac{1}{2}$$\overrightarrow{c}$ |
3.已知圆锥的母线长是10,侧面展开图是半圆,则该圆锥的侧面积为( )
| A. | $\frac{100}{3}$π | B. | 100π | C. | $\frac{50}{3}$π | D. | 50π |