题目内容
用三种不同的颜色，将如图所示的4个区域涂色，每种颜色至少用1次，则相邻的区域不涂同一种颜色的概率为考点：古典概型及其概率计算公式
专题：计算题
分析：不妨从左至右按1-4编号，由于三种颜色必须用全，第一步涂一号有三种涂法，第二步涂二号有二种涂法第三步涂三号时可分为两类研究，然后利用古典概型的概率公式进行求解即可．
解答：
解：由题意，不妨从左至右按1-4编号，由于三种颜色必须用全，第一步涂一号有三种涂法，第二步涂二号有二种涂法第三步涂三号时可分为两类研究，故总的涂色方法为3×2×（1×1+1×2）=18种，
所有情形有
=6×6=36，
所以相邻的区域不涂同一种颜色的概率为
=
．
所有情形有
| C | 2 4 |
| A | 3 3 |
所以相邻的区域不涂同一种颜色的概率为
| 18 |
| 36 |
| 1 |
| 2 |
点评：本题考查计数原理的应用和概率的计算，解题的关键是理解题意，根据题设中涂色要求选择用分步原理计数，由于本题要求三种颜色必须全用上，答题时易漏掉这一限制条件导致计数出错，这是本题的易错点，解题时认真审题，考虑全面是做对本题的重点，本题解题方法上大的方面是分步原理，在其中也用到了分类原理，对计数原理考查全面，此种题已多次出现在高考试卷上，要注意总结它的解题规律，分析清楚分类与分步的依据．
练习册系列答案
相关题目
已知椭圆：
+
=1的焦距为4，则m等于（ ）
| x2 |
| 10-m |
| y2 |
| m-2 |
| A、4 | B、8 |
| C、4或8 | D、以上均不对 |
下列四个方程中表示y是x的函数的是（ ）
①x-2y=6②x2+y=1③x+y2=1④x=
．
①x-2y=6②x2+y=1③x+y2=1④x=
| y |
| A、①② | B、①④ | C、③④ | D、①②④ |
设集合M={x|0≤x≤2}，N={y|0≤y≤2}，给出下列4个图形，其中能表示集合M到N的函数关系的有（ ）
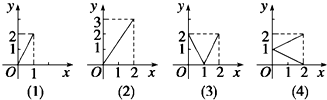
| A、0个 | B、1个 | C、2个 | D、3个 |
已知f(
)=
，则f（x）=（ ）
| 1 |
| x |
| 1 |
| x+1 |
A、
| ||
B、
| ||
C、
| ||
| D、1+x |