题目内容
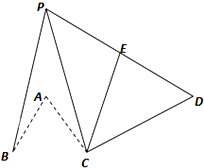 在如图所示的四棱锥P-ABCD中,已知PA⊥平面ABCD,AD∥BC,∠BAD=90°,PA=AB=BC=1,AD=2,E为PD的中点.
在如图所示的四棱锥P-ABCD中,已知PA⊥平面ABCD,AD∥BC,∠BAD=90°,PA=AB=BC=1,AD=2,E为PD的中点.(Ⅰ)求异面直线PC与AD所成的角;
(Ⅱ)求证:平面PAC⊥平面PDC;
(Ⅲ)求直线EC与平面PAC所成角的余弦值.
考点:直线与平面所成的角,异面直线及其所成的角,平面与平面垂直的判定
专题:空间角
分析:
要求异面直线所成的角,要先找到这个角,通过条件能找到直线PC与AD所成的角是∠PCB,根据条件求出即可.证明平面和平面垂直,根据面面垂直的判定定理,需从一个平面内找到一条直线,让它和另一平面垂直.根据条件PA⊥平面ABCD,所以得到PA⊥DC,即DC⊥PA,那么这时候想着,看CD能不能垂直于AC,然后根据条件是可以的.第三问是求线面角,要先找到这个角,通过观察图形会发现取PC边的中点,∠ECE′便是所找的角.
解答:
(Ⅰ)解:如图,∵AD∥BC∴异面直线PC与AD所成的角即是直线PC与BC所成的角,

所以∠PCB即是异面直线PC与AD所成的角;
∵PA⊥平面ABCD,
∴PA⊥AB,PA⊥AD,即AD⊥PA,又∠BAD=90°,∴AD⊥AB;
∴AD⊥平面PAB,∴BC⊥平面PAB;
∴△PBC是直角三角形;
∴根据条件,PB=
,tan∠PCB=
;
∴异面直线PC与AD所成的角是arctan
.
(Ⅱ)证明:连接AC,∵PA⊥平面ABCD;
∴PA⊥DC,即DC⊥PA;
过C作CC′⊥AD,交AD于C′,则CC′=1,C′D=1,∴CD=
;
又AC=
,∴AC2+CD2=2+2=AD2
∴DC⊥AC;
∵AC∩PA=A;
∴DC⊥平面PAC;
又DC?平面PDC;
所以平面PAC⊥平面PDC.
(Ⅲ)取PC中点E′,则EE′∥DC,
由(Ⅱ)知DC⊥平面PAC
则EF⊥平面PAC
所以∠ECE′为直线EC与平面PAC所成的角
CE′=
,EF=
;
∴EC=
,∴cos∠ECE′=
;
即直线EC与平面PAC所成角的余弦值是
.

所以∠PCB即是异面直线PC与AD所成的角;
∵PA⊥平面ABCD,
∴PA⊥AB,PA⊥AD,即AD⊥PA,又∠BAD=90°,∴AD⊥AB;
∴AD⊥平面PAB,∴BC⊥平面PAB;
∴△PBC是直角三角形;
∴根据条件,PB=
| 2 |
| 2 |
∴异面直线PC与AD所成的角是arctan
| 2 |
(Ⅱ)证明:连接AC,∵PA⊥平面ABCD;
∴PA⊥DC,即DC⊥PA;
过C作CC′⊥AD,交AD于C′,则CC′=1,C′D=1,∴CD=
| 2 |
又AC=
| 2 |
∴DC⊥AC;
∵AC∩PA=A;
∴DC⊥平面PAC;
又DC?平面PDC;
所以平面PAC⊥平面PDC.
(Ⅲ)取PC中点E′,则EE′∥DC,
由(Ⅱ)知DC⊥平面PAC
则EF⊥平面PAC
所以∠ECE′为直线EC与平面PAC所成的角
CE′=
| ||
| 2 |
| ||
| 2 |
∴EC=
| ||
| 2 |
| ||
| 5 |
即直线EC与平面PAC所成角的余弦值是
| ||
| 5 |
点评:考查的知识点有:异面直线所成角,面面垂直的判定定理,线面垂直的判定定理,线面角的定义.这里要注意的是,若求的是角,需先找到这个角,然后根据条件求出即可;而要判断垂直问题,找判定定理所需具备的条件.

练习册系列答案
 期末宝典单元检测分类复习卷系列答案
期末宝典单元检测分类复习卷系列答案
相关题目
(
+
)5展开式的常数项为80,则a的值为( )
| x |
| a | |||
|
| A、1 | ||
| B、2 | ||
C、
| ||
| D、4 |
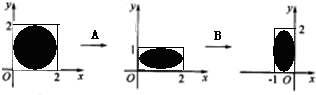 二阶矩阵A,B对应的变换对圆的区域作用结果如图所示.
二阶矩阵A,B对应的变换对圆的区域作用结果如图所示.