题目内容
对于函数f(x)=
,x∈(-
,0)∪(0,
),对于区间(-
,0)∪(0,
)上的任意实数x1,x2,有如下条件:(1)x1>x2;(2)x12>x22;(3)|x1|>x2;(4)x1+x2<0;(5)x1>|x2|,其中能使f(x1)<f(x2)恒成立的条件的序号有 .(写出你认为成立的所有条件序号)
| sinx |
| x |
| π |
| 2 |
| π |
| 2 |
| π |
| 2 |
| π |
| 2 |
考点:利用导数研究函数的单调性
专题:综合题,函数的性质及应用,导数的综合应用
分析:利用导数可以判定其单调性,再判断出奇偶性,逐项分析可判断出结论.
解答:
解:f′(x)=
,
令g(x)=xcosx-sinx,则g′(x)=cosx-xsinx-cosx=-xsinx,
当x∈(0,
)时,g′(x)<0,g(x)递减,
∴g(x)<g(0)=0,f′(x)<0,
∴f(x)在(0,
)上单调递减,
又f(-x)=f(x),∴f(x)为偶函数,在(-
,0)上递增.
(1)x1>x2,f(x1)<f(x2)不成立;
(2)由x12>x22,得|x1|>|x2|,∴f(|x1|)<f(|x2|),即f(x1)<f(x2)成立;
(3)|x1|>x2,取x1=-
,x2=-1,则f(x1)<f(x2)不成立;
(4)x1+x2<0,取x1=-
,x2=-1,则f(x1)<f(x2)不成立;
(5)x1>|x2|,即|x1|>|x2|,由(2)知f(x1)<f(x2)成立;
故答案为:②⑤.
| xcosx-sinx |
| x2 |
令g(x)=xcosx-sinx,则g′(x)=cosx-xsinx-cosx=-xsinx,
当x∈(0,
| π |
| 2 |
∴g(x)<g(0)=0,f′(x)<0,
∴f(x)在(0,
| π |
| 2 |
又f(-x)=f(x),∴f(x)为偶函数,在(-
| π |
| 2 |
(1)x1>x2,f(x1)<f(x2)不成立;
(2)由x12>x22,得|x1|>|x2|,∴f(|x1|)<f(|x2|),即f(x1)<f(x2)成立;
(3)|x1|>x2,取x1=-
| 1 |
| 2 |
(4)x1+x2<0,取x1=-
| 1 |
| 2 |
(5)x1>|x2|,即|x1|>|x2|,由(2)知f(x1)<f(x2)成立;
故答案为:②⑤.
点评:熟练掌握利用导数研究函数的单调性、判定函数的奇偶性等是解题的关键.

练习册系列答案
 星级口算天天练系列答案
星级口算天天练系列答案 芒果教辅达标测试卷系列答案
芒果教辅达标测试卷系列答案
相关题目
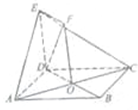 如图,O为正方形ABCD的中心,四边形ODEF是平行四边形,且平面ODEF⊥平面ABCD,AD=2,DE=
如图,O为正方形ABCD的中心,四边形ODEF是平行四边形,且平面ODEF⊥平面ABCD,AD=2,DE=