题目内容
已知点A(-1,0)、B(1,0),动点P满足:∠APB=2θ,且|PA|•|PB|cos2θ=1
(1)求动点P的轨迹C的方程;
(2)已知圆W:x2+y2=
的切线l与轨迹C相交于P,Q两点,求证:以PQ为直径的圆经过坐标原点O.
(1)求动点P的轨迹C的方程;
(2)已知圆W:x2+y2=
| 2 |
| 3 |
考点:直线与圆锥曲线的综合问题
专题:圆锥曲线中的最值与范围问题
分析:(1)当点P在线段AB上时,动点P的轨迹不存在;当点P在x轴上且在线段AB外时,P(±
,0);当点P不在x轴上时,由余弦定理得动点P在以A、B为两焦点的椭圆上,由此能求出动点P的轨迹C的方程.
(2)当直线l的斜率不存在或为0时,以PQ为直径的圆的方程经过坐标原点O;当直线l的斜率存在且不为零时.设直线l的方程为y=kx+m.由
,得(2k2+1)x2+4kmx+2m2-2=0.由此能求出以PQ为直径的圆经过坐标原点O.故以PQ为直径的圆经过坐标原点O.
| 2 |
(2)当直线l的斜率不存在或为0时,以PQ为直径的圆的方程经过坐标原点O;当直线l的斜率存在且不为零时.设直线l的方程为y=kx+m.由
|
解答:
(1)解:①当点P在线段AB上时,
θ不存在或θ=
,均不满足题目条件;(1分)
②当点P在x轴上且在线段AB外时,
θ=0,设P(p,0),
由|PA|•|PB|cos2θ=1,得(p+1)(p-1)=1,
∴p=±
,∴P(±
,0);(3分)
③当点P不在x轴上时,
在△PAB中,由余弦定理得|AB|2=|PA|2+|PB|2-2|PA|•|PB|cos2θ,
∴4=(|PA|+|PB|)2-2|PA|•|PB|(1+cos2)
=(|PA|+|PB|)2-4|PA|•|PB|cos2θ
=(|PA|+|PB|)2-4,∴|PA|+|PB|=2
>2=|AB|,
即动点P在以A、B为两焦点的椭圆上.
方程为:
+y2=1.(x≠±
)
综合①②③可知:动点P的轨迹C的方程为:
+y2=1.(6分)
(2)证明:①当直线l的斜率不存在时.
∵直线l与圆W相切,故切线方程为x=
或x=-
,
切线方程与
+y2=1联立方程组,
求得P,Q为(
,±
)或P,Q为(-
,±
),
则以PQ为直径的圆的方程为(x±
)2+y2=
,经过坐标原点O.
②当直线l的斜率为零时.
与①类似,求得以PQ为直径的圆的方程为x2+(y±
)2=
,经过坐标原点O.(10分)
③当直线l的斜率存在且不为零时.设直线l的方程为y=kx+m.
由
消去y,得(2k2+1)x2+4kmx+2m2-2=0.
设P(x1,y1),Q(x2,y2),
则x1+x2=
,x1•x2=
.
∴y1y2=(kx1+m)(kx2+m)=k2x1x2+km(x1+x2)+m2=
.
∴
•
=x1x2+y1y2=
.①
∵直线l和圆W相切,
∴圆心到直线l的距离d=
=
,整理得m2=
(1+k2).②
将②式代入①式,得
•
=0,显然以PQ为直径的圆经过坐标原点O.
综上可知,以PQ为直径的圆经过坐标原点O.(14分)
θ不存在或θ=
| π |
| 2 |
②当点P在x轴上且在线段AB外时,
θ=0,设P(p,0),
由|PA|•|PB|cos2θ=1,得(p+1)(p-1)=1,
∴p=±
| 2 |
| 2 |
③当点P不在x轴上时,
在△PAB中,由余弦定理得|AB|2=|PA|2+|PB|2-2|PA|•|PB|cos2θ,
∴4=(|PA|+|PB|)2-2|PA|•|PB|(1+cos2)
=(|PA|+|PB|)2-4|PA|•|PB|cos2θ
=(|PA|+|PB|)2-4,∴|PA|+|PB|=2
| 2 |
即动点P在以A、B为两焦点的椭圆上.
方程为:
| x2 |
| 2 |
| 2 |
综合①②③可知:动点P的轨迹C的方程为:
| x2 |
| 2 |
(2)证明:①当直线l的斜率不存在时.
∵直线l与圆W相切,故切线方程为x=
| ||
| 3 |
| ||
| 3 |
切线方程与
| x2 |
| 2 |
求得P,Q为(
| ||
| 3 |
| ||
| 3 |
| ||
| 3 |
| ||
| 3 |
则以PQ为直径的圆的方程为(x±
| ||
| 3 |
| 2 |
| 3 |
②当直线l的斜率为零时.
与①类似,求得以PQ为直径的圆的方程为x2+(y±
| ||
| 3 |
| 2 |
| 3 |
③当直线l的斜率存在且不为零时.设直线l的方程为y=kx+m.
由
|
设P(x1,y1),Q(x2,y2),
则x1+x2=
| -4km |
| 2k2+1 |
| 2m2-2 |
| 2k2+1 |
∴y1y2=(kx1+m)(kx2+m)=k2x1x2+km(x1+x2)+m2=
| m2-2k2 |
| 2k2+1 |
∴
| OP |
| OQ |
| 3m2-2k2-2 |
| 2k2+1 |
∵直线l和圆W相切,
∴圆心到直线l的距离d=
| |m| | ||
|
| ||
| 3 |
| 2 |
| 3 |
将②式代入①式,得
| OP |
| OQ |
综上可知,以PQ为直径的圆经过坐标原点O.(14分)
点评:本题考查椭圆方程的求法,考查圆经过坐标原点的证明,解题时要认真审题,注意分类讨论思想的合理运用.

练习册系列答案
相关题目
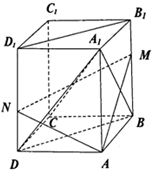 如图,长方体ABCD-A1B1C1D1中,点M,N分别在BB1,DD1上,且AM⊥A1B,AN⊥A1D.
如图,长方体ABCD-A1B1C1D1中,点M,N分别在BB1,DD1上,且AM⊥A1B,AN⊥A1D.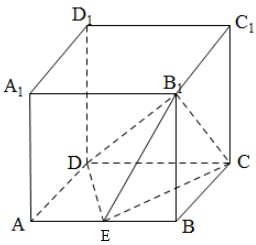
 如图,在直三棱柱ABC-A1B1C1中,∠ABC=90°,AB=BC=BB1=1,D是A1C的中点.
如图,在直三棱柱ABC-A1B1C1中,∠ABC=90°,AB=BC=BB1=1,D是A1C的中点.