题目内容
6.已知平面向量$\overrightarrow a$和$\overrightarrow b$的夹角为60°,$\overrightarrow a=(2,0)$,$|\overrightarrow b|=1$,则$|\overrightarrow a+2\overrightarrow b|$=( )| A. | 20 | B. | 12 | C. | $4\sqrt{3}$ | D. | $2\sqrt{3}$ |
分析 根据向量数量积的定义先求出$\overrightarrow{a}•\overrightarrow{b}$=1,然后利用向量模长与向量数量积的关系进行转化求解即可.
解答 解:向量$\overrightarrow a$和$\overrightarrow b$的夹角为60°,$\overrightarrow a=(2,0)$,$|\overrightarrow b|=1$,
∴|$\overrightarrow{a}$|=2,$\overrightarrow{a}•\overrightarrow{b}$=2×1×$\frac{1}{2}$=1,
∴$|\overrightarrow a+2\overrightarrow b|$2=${\overrightarrow{a}}^{2}$+4$\overrightarrow{a}•\overrightarrow{b}$+4${\overrightarrow{b}}^{2}$=4+4+4=12,
∴$|\overrightarrow a+2\overrightarrow b|$=2$\sqrt{3}$,
故选:D
点评 本题主要考查向量数量积的应用,根据向量数量积的定义以及向量模长的公式是解决本题的关键.

练习册系列答案
相关题目
11.已知双曲线$\frac{x^2}{a^2}-\frac{y^2}{b^2}=1$(a>0,b>0)的两条渐进线与抛物线y2=4x的准线分别交于A,B两点,O为坐标原点,若${S_{△AOB}}=2\sqrt{3}$,则双曲线的离心率e=( )
| A. | $\frac{3}{2}$ | B. | $\frac{{\sqrt{7}}}{2}$ | C. | 2 | D. | $\sqrt{13}$ |
16.已知函数f(x)=-sin(x+$\frac{π}{2}$),(x∈R),下面结论错误的是( )
| A. | 函数f(x)的最小正周期为2π | B. | 函数f(x)在区间[0,$\frac{π}{2}$]上是增函数 | ||
| C. | 函数f(x)的图象关于直线x=0对称 | D. | 函数f(x)是奇函数 |
17.如图所示是正三棱锥V-ABC的正视图,侧视图和俯视图,则其正视图的面积为( ) 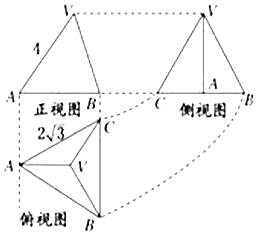

| A. | 6 | B. | 5 | C. | 4$\sqrt{3}$ | D. | 3$\sqrt{3}$ |