题目内容
设数列{an},其前n项和Sn=-3n2,{bn}为单调递增的等比数列,b1b2b3=512,a1+b1=a3+b3.
(1)求数列{an},{bn}的通项;
(2)若cn=
,数列{cn}的前n项和Tn,求证:
≤Tn<1.
(1)求数列{an},{bn}的通项;
(2)若cn=
| bn |
| (bn-2)(bn-1) |
| 2 |
| 3 |
考点:数列与不等式的综合
专题:等差数列与等比数列
分析:(1)由已知得a1=-3,当n≥2时,an=Sn-Sn-1=(-3n2+3(n-1)2=-6n+3,由此能求出an=-6n+3;由已知得
,由此能求出bn=2n+1.
(2)cn=
=
=
-
,由此利用裂项求和法能证明
≤Tn<1.
|
(2)cn=
| 2n+1 |
| (2n+1-2)(2n+1-1) |
| 2n |
| (2n-1)(2n+1-1) |
| 1 |
| 2n-1 |
| 1 |
| 2n+1-1 |
| 2 |
| 3 |
解答:
(1)解:∵数列{an},其前n项和Sn=-3n2,
∴a1=-3,
当n≥2时,an=Sn-Sn-1=(-3n2+3(n-1)2=-6n+3,
当n=1时,上式也成立,
∴an=-6n+3,
∵{bn}为单调递增的等比数列,b1b2b3=512,a1+b1=a3+b3,
∴
,
解得b1=4,q=2或b1=-16,q=-
(舍),
∴bn=2n+1.(4分)
(2)证明:cn=
=
=
-
(8分)
∴Tn=c1+c2+c3+…+cn
=(
-
)+(
-
)+…+(
-
)
=1-
∵{ Tn } 是递增数列,(12分)
∴
≤Tn<1(14分)
∴a1=-3,
当n≥2时,an=Sn-Sn-1=(-3n2+3(n-1)2=-6n+3,
当n=1时,上式也成立,
∴an=-6n+3,
∵{bn}为单调递增的等比数列,b1b2b3=512,a1+b1=a3+b3,
∴
|
解得b1=4,q=2或b1=-16,q=-
| 1 |
| 2 |
∴bn=2n+1.(4分)
(2)证明:cn=
| 2n+1 |
| (2n+1-2)(2n+1-1) |
| 2n |
| (2n-1)(2n+1-1) |
| 1 |
| 2n-1 |
| 1 |
| 2n+1-1 |
∴Tn=c1+c2+c3+…+cn
=(
| 1 |
| 2-1 |
| 1 |
| 22-1 |
| 1 |
| 22-1 |
| 1 |
| 23-1 |
| 1 |
| 2n-1 |
| 1 |
| 2n+1-1 |
=1-
| 1 |
| 2n+1-1 |
∵{ Tn } 是递增数列,(12分)
∴
| 2 |
| 3 |
点评:本题考查数列的通项公式的求法,考查不等式的证明,解题时要认真审题,注意裂项求和法的合理运用.

练习册系列答案
相关题目
若{1,2}⊆A⊆{1,2,3,4,5}}则满足条件的集合A的个数是( )
| A、6 | B、7 | C、8 | D、9 |
已知直线y=x+1与曲线y=ex+a相切,则a的值为( )
| A、1 | B、2 | C、-1 | D、0 |
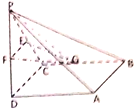 如图所示,在四棱锥P-ABCD中,底面ABCD为正方形,如果PD⊥平面ABCD,PD=AB=2,E,F,G分别为PC,PD,BC的中点
如图所示,在四棱锥P-ABCD中,底面ABCD为正方形,如果PD⊥平面ABCD,PD=AB=2,E,F,G分别为PC,PD,BC的中点