题目内容
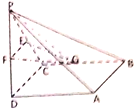 如图所示,在四棱锥P-ABCD中,底面ABCD为正方形,如果PD⊥平面ABCD,PD=AB=2,E,F,G分别为PC,PD,BC的中点
如图所示,在四棱锥P-ABCD中,底面ABCD为正方形,如果PD⊥平面ABCD,PD=AB=2,E,F,G分别为PC,PD,BC的中点(Ⅰ)求证:PA∥平面EFG;
(Ⅱ)求证:CG⊥平面PCD,并求P-EFG三棱锥的体积.
考点:直线与平面垂直的判定,直线与平面平行的判定
专题:空间位置关系与距离
分析:(Ⅰ)先由PB∥平面EFG,AB∥平面EFG证明平面PAB∥平面EFG,再证明PA∥平面EFG;
(Ⅱ)由PD⊥CG,CG⊥CD,证明CG⊥平面PCD;
由V三棱锥P-EFG=V三棱锥G-PEF,求出△PEF的面积S△PEF以及棱锥的高CG即可求出体积.
(Ⅱ)由PD⊥CG,CG⊥CD,证明CG⊥平面PCD;
由V三棱锥P-EFG=V三棱锥G-PEF,求出△PEF的面积S△PEF以及棱锥的高CG即可求出体积.
解答:
解:(Ⅰ)证明:∵PB∥EG,PB?平面EFG,
∴PB∥平面EFG;-----(2分)
又∵AB∥DC,EF∥DC,
∴AB∥EF,
且AB?平面EFG,∴AB∥平面EFG;----(4分)
又∵PB∩AB=B,∴平面PAB∥平面EFG;-----(6分)
∴PA∥平面EFG;----(7分)
(Ⅱ)证明:∵PD⊥平面ABCD,CG?平面ABCD,
∴PD⊥CG;-------(9分)
又∵CG⊥CD,且PD∩CD=D,
∴CG⊥平面PCD;------(11分)
又∵PF=EF=
PA=1,CG=
DA=1,
∴V三棱锥P-EFG=V三棱锥G-PEF
=
S△PEF•CG
=
×
×1×1×1
=
.-----(14分)
∴PB∥平面EFG;-----(2分)
又∵AB∥DC,EF∥DC,
∴AB∥EF,
且AB?平面EFG,∴AB∥平面EFG;----(4分)
又∵PB∩AB=B,∴平面PAB∥平面EFG;-----(6分)
∴PA∥平面EFG;----(7分)
(Ⅱ)证明:∵PD⊥平面ABCD,CG?平面ABCD,
∴PD⊥CG;-------(9分)
又∵CG⊥CD,且PD∩CD=D,
∴CG⊥平面PCD;------(11分)
又∵PF=EF=
| 1 |
| 2 |
| 1 |
| 2 |
∴V三棱锥P-EFG=V三棱锥G-PEF
=
| 1 |
| 3 |
=
| 1 |
| 3 |
| 1 |
| 2 |
=
| 1 |
| 6 |
点评:本题考查了空间中的平行与垂直的证明问题,解题时应熟练地运用几何语言、符号语言和图形语言进行解答,是中档题.

练习册系列答案
 小学夺冠AB卷系列答案
小学夺冠AB卷系列答案
相关题目
过定点P(2,1),且倾斜角是直线l:x-y-1=0的倾斜角两倍的直线方程为( )
| A、x-2y-1=0 |
| B、2x-y-1=0 |
| C、y-1=2(x-2) |
| D、x=2 |
执行如图所示的程序框图,若输出的结果是7,则判断框内m的取值范围是( )


| A、(30,42] |
| B、(42,56] |
| C、(56,72] |
| D、(72,90] |