题目内容
由y=x2,y=x所围成的图形绕y轴旋转所得到的旋转体的体积V= .
考点:用定积分求简单几何体的体积
专题:计算题,导数的概念及应用
分析:求出曲线y=x2与直线y=x交点O、A的坐标,结合旋转体的积分计算公式,可得所求旋转体的体积等于函数y=π(y-y2)在[0,1]上的积分值,再用定积分计算公式加以计算即可得到该旋转体的体积.
解答:
解:∴曲线y=x2与直线y=x交于点O(0,0)和A(1,1)
∴根据旋转体的积分计算公式,可得
该旋转体的体积为V=
π(y-y2)dy=π(
y3-
y3)
=
,
故答案为:
.
∴根据旋转体的积分计算公式,可得
该旋转体的体积为V=
| ∫ | 1 0 |
| 1 |
| 2 |
| 1 |
| 3 |
| | | 1 0 |
| π |
| 6 |
故答案为:
| π |
| 6 |
点评:本题给出曲线y=x2与直线y=x所围成的平面图形,求该图形绕y轴转一周得到旋转体的体积.着重考查了利用定积分公式计算由曲边图形旋转而成的几何体体积的知识,属于基础题.

练习册系列答案
 100分闯关期末冲刺系列答案
100分闯关期末冲刺系列答案
相关题目
函数y=ecosx(-π≤x≤π)的大致图象为( )
A、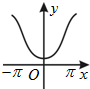 |
B、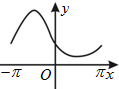 |
C、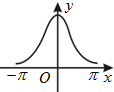 |
D、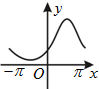 |
若集合A={x||x|<1},B={x|x2-2x<0},则A∩B=( )
| A、(-1,2) |
| B、(0,1) |
| C、(0,2) |
| D、(1,2) |
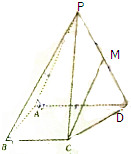 如图,在四棱锥P-ABCD中,平面PAD⊥平面ABCD,△PAD是等边三角形,AD∥BC,∠ABC=90°,M是PD的中点,且AD=2AB=2BC=2.
如图,在四棱锥P-ABCD中,平面PAD⊥平面ABCD,△PAD是等边三角形,AD∥BC,∠ABC=90°,M是PD的中点,且AD=2AB=2BC=2.