题目内容
若方程(m2-3m+2)x+(m-2)y-2m+5=0表示直线.
(1)求实数m的值;
(2)若该直线的斜率k<1,求实数m的范围.
(1)求实数m的值;
(2)若该直线的斜率k<1,求实数m的范围.
考点:直线的斜率
专题:直线与圆
分析:(1)由直线方程的特点可得(m2-3m+2)和(m-2)不同时为0,进而解得m≠2;
(2)若该直线的斜率k<1,则m≠2且
<1,解不等式可得.
(2)若该直线的斜率k<1,则m≠2且
| m2-3m+2 |
| m-2 |
解答:
解:(1)∵方程(m2-3m+2)x+(m-2)y-2m+5=0表示直线,
∴(m2-3m+2)和(m-2)不同时为0,即(m2-3m+2)2+(m-2)2≠0,
解得m≠2,∴实数m的值为m≠2;
(2)若该直线的斜率k<1,则m≠2且
<1,
∴
-1<0,即m-2<0,解得m<2
∴实数m的范围为m<2
∴(m2-3m+2)和(m-2)不同时为0,即(m2-3m+2)2+(m-2)2≠0,
解得m≠2,∴实数m的值为m≠2;
(2)若该直线的斜率k<1,则m≠2且
| m2-3m+2 |
| m-2 |
∴
| m2-3m+2 |
| m-2 |
∴实数m的范围为m<2
点评:本题考查直线的斜率和直线方程的特点,属基础题.

练习册系列答案
 期末1卷素质教育评估卷系列答案
期末1卷素质教育评估卷系列答案
相关题目
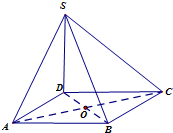 如图,四棱锥S-ABCD的底面为正方形,SD⊥底面ABCD,给出下列结论:①AC⊥SB;②AB∥平面SCD;③SA与平面ABD所成的角等于SC与平面ABD所成的角;④AC⊥SO;⑤AB与SC所成的角等于DC与SA所成的角其中,正确结论的序号是
如图,四棱锥S-ABCD的底面为正方形,SD⊥底面ABCD,给出下列结论:①AC⊥SB;②AB∥平面SCD;③SA与平面ABD所成的角等于SC与平面ABD所成的角;④AC⊥SO;⑤AB与SC所成的角等于DC与SA所成的角其中,正确结论的序号是