题目内容

用lgx，lgy，lgz表示lg
x
y
z2
=
 
．
考点：对数的运算性质
专题：函数的性质及应用
分析：由对数的运算性质逐步化简即可．
解答： 解：由对数的运算性质可得lg
x
y
z2

=lg（x
y
）-lgz2=lgx+lg
y
-2lgz
=lgx+
1
2
lgy-2lgz，
故答案为：lgx+
1
2
lgy-2lgz，
点评：本题考查对数的运算性质，属基础题．
练习册系列答案
相关题目
P是椭圆
x2
16
+
y2
9
=1上一点，F1、F2分别是椭圆的左、右焦点，若|PF1|•|PF2|=12，则∠F1PF2的大小为（　　）
A、30°B、60°
C、120°D、150°
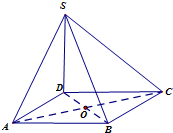如图，四棱锥S-ABCD的底面为正方形，SD⊥底面ABCD，给出下列结论：①AC⊥SB；②AB∥平面SCD；③SA与平面ABD所成的角等于SC与平面ABD所成的角；④AC⊥SO；⑤AB与SC所成的角等于DC与SA所成的角其中，正确结论的序号是
 
．
证明下列恒等式：
（1）（cosα-1）2+sin2α=2-2cosα；
（2）（tan2α-sin2α）cot2α=sin2α；
（3）（cosα-cosβ）2+（sinα-sinβ）2=2-2（cosαcosβ+sinαsinβ）；
（4）
1+cot2α
1-cot2α
=
1
2sin2α-1
．
函数f（x）=
x+1(x＞0)
a(x=0)
x-1(x＜0)
在R上是单调增函数，则a的取值集合为
 
．
证明三角恒等式：
tanasina
tana-sina
=
tana+sina
tanasina
．
被n整除得n+3的数是
 
．
已知函数f（x）=loga|bx|（其中a＞0，b＞0，且a≠1）函数的图象经过两点（1，0），（4，2）．
（1）求实数a，b的值，并写出函数的解析式；
（2）判断f（x）的奇偶性．
已知函数f（x）=ax3+bx2+cx+d（a≠0）的对称中心为M（x0，y0），记函数f（x）的导函数为f′（x），f′（x）的导函数为f″（x），则有f″（x）=0．若函数f（x）=x3-3x2，则可求出f（
1
2014
）+f（
2
2014
）+f（
3
2014
）+…+f（
4026
2014
）+f（
4027
2014
）的值为
 
．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网