题目内容
求解不等式:
(1)(x+5)(4-x)(x-2)≥0
(2)(x-4)(x+1)(x2-4x+4)≤0.
(1)(x+5)(4-x)(x-2)≥0
(2)(x-4)(x+1)(x2-4x+4)≤0.
考点:其他不等式的解法
专题:不等式的解法及应用
分析:根据不等式关系将不等式进行转化即可得到结论.
解答:
解:(1)不等式(x+5)(4-x)(x-2)≥0等价为
或
,
即
或
,
即x≤-5或2≤x≤4,
即不等式的解集为{x|x≤-5或2≤x≤4}
(2)不等式(x-4)(x+1)(x2-4x+4)≤0等价为(x-4)(x+1)(x-2)2≤0,
若x=2,则不等式成立,
当x≠0时,不等式等价为(x-4)(x+1)≤0,
即-1≤x≤4且x≠0,
故不等式的解集为{x|-1≤x≤4且x≠0}.
|
|
即
|
|
即x≤-5或2≤x≤4,
即不等式的解集为{x|x≤-5或2≤x≤4}
(2)不等式(x-4)(x+1)(x2-4x+4)≤0等价为(x-4)(x+1)(x-2)2≤0,
若x=2,则不等式成立,
当x≠0时,不等式等价为(x-4)(x+1)≤0,
即-1≤x≤4且x≠0,
故不等式的解集为{x|-1≤x≤4且x≠0}.
点评:本题主要考查不等式的求解,将不等式进行转化为不等式组是解决本题的关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
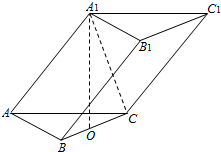 在三棱柱ABC-A1B1C1中,已知AB=AC=AA1=
在三棱柱ABC-A1B1C1中,已知AB=AC=AA1=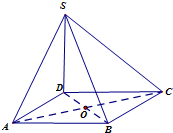 如图,四棱锥S-ABCD的底面为正方形,SD⊥底面ABCD,给出下列结论:①AC⊥SB;②AB∥平面SCD;③SA与平面ABD所成的角等于SC与平面ABD所成的角;④AC⊥SO;⑤AB与SC所成的角等于DC与SA所成的角其中,正确结论的序号是
如图,四棱锥S-ABCD的底面为正方形,SD⊥底面ABCD,给出下列结论:①AC⊥SB;②AB∥平面SCD;③SA与平面ABD所成的角等于SC与平面ABD所成的角;④AC⊥SO;⑤AB与SC所成的角等于DC与SA所成的角其中,正确结论的序号是