题目内容
求下列函数的极值
(1)y=(x-1)
(2)y=x-ln(1+x)
(1)y=(x-1)
| 3 | x3 |
(2)y=x-ln(1+x)
考点:利用导数研究函数的极值
专题:计算题,函数的性质及应用,导数的综合应用
分析:(1)化简y=(x-1)
=(x-1)x,由二次函数的性质求极值;
(2)求导y′=1-
,由导数求极值.
| 3 | x3 |
(2)求导y′=1-
| 1 |
| 1+x |
解答:
解:(1)y=(x-1)
=(x-1)x,
则由二次函数的性质可知,
函数在x=
处取得极小值,
即极小值为y=-
×
=-
;
(2)y=x-ln(1+x),
y′=1-
,
则当x=0时,函数取得极小值,
即极小值为0-0=0.
| 3 | x3 |
则由二次函数的性质可知,
函数在x=
| 1 |
| 2 |
即极小值为y=-
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 4 |
(2)y=x-ln(1+x),
y′=1-
| 1 |
| 1+x |
则当x=0时,函数取得极小值,
即极小值为0-0=0.
点评:本题考查了函数的极值的求法,属于中档题.

练习册系列答案
 新课标快乐提优暑假作业陕西旅游出版社系列答案
新课标快乐提优暑假作业陕西旅游出版社系列答案
相关题目
命题“?x∈R,x≥sinx”的否定是( )
| A、?x∈R,x<sinx |
| B、?x∈R,x≤sinx |
| C、?x∈R,x<sinx |
| D、?x∈R,x<sinx |
P是椭圆
+
=1上一点,F1、F2分别是椭圆的左、右焦点,若|PF1|•|PF2|=12,则∠F1PF2的大小为( )
| x2 |
| 16 |
| y2 |
| 9 |
| A、30° | B、60° |
| C、120° | D、150° |
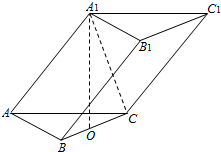 在三棱柱ABC-A1B1C1中,已知AB=AC=AA1=
在三棱柱ABC-A1B1C1中,已知AB=AC=AA1=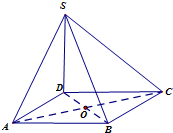 如图,四棱锥S-ABCD的底面为正方形,SD⊥底面ABCD,给出下列结论:①AC⊥SB;②AB∥平面SCD;③SA与平面ABD所成的角等于SC与平面ABD所成的角;④AC⊥SO;⑤AB与SC所成的角等于DC与SA所成的角其中,正确结论的序号是
如图,四棱锥S-ABCD的底面为正方形,SD⊥底面ABCD,给出下列结论:①AC⊥SB;②AB∥平面SCD;③SA与平面ABD所成的角等于SC与平面ABD所成的角;④AC⊥SO;⑤AB与SC所成的角等于DC与SA所成的角其中,正确结论的序号是