题目内容

7．已知全集U为实数集，集合A={x|x2-2x-3＜0}，B={x|x＜1}，则A∩B为（　　）
A．{x|1≤x＜3}B．{x|x＜3}C．{x|x≤-1}D．{x|-1＜x＜1}

分析 求出关于A的不等式，求出A、B的交集即可．

解答 解：A={x|x2-2x-3＜0}={x|-1＜x＜3}，
B={x|x＜1}，
∴A∩B={x|-1＜x＜1}，
故选：D．

点评 本题考查了集合的运算，考查不等式问题，是一道基础题．

练习册系列答案
相关题目
17．执行如图的程序框图，若输入的a，b的值分别为0和9，则输出的i的值为（　　）
A．1B．2C．3D．4
18．已知$\overrightarrow a，\overrightarrow b$为单位向量，若|$\overrightarrow{a}$+$\overrightarrow{b}$|=|$\overrightarrow{a}$-$\overrightarrow{b}$|，则$\overrightarrow{a}$在$\overrightarrow{a}$+$\overrightarrow{b}$方向上的投影为$\frac{\sqrt{2}}{2}$．
15．已知函数f（x），g（x）分别是定义在R上的偶函数和奇函数，且f（x）+g（x）=2x+x，则f（log23）=$\frac{5}{3}$．
2．设等差数列{an}的前n项和Sn满足S5=15，且2a2，a6，a8+1成公比大于1的等比数列．
（1）求数列{an}的通项公式；
（2）设${b_n}=\frac{a_n}{2^n}$，求数列{bn}的前n项和Tn．
12．2016年某省人社厅推出15项改革措施，包括机关事业单位基本养老保险制度改革、调整机关事业单位工资标准、全省县以下机关建立职务与职级并行制度．某市为了了解该市市民对这些改革措施的态度，在该市随机抽取了50名市民进行调查，作出了他们月收入（单位：百元，范围：[15，75]）的频率分布直方图，同时得到其中各种月收入情况的市民对该项政策赞成的人数统计表．
月收入赞成人数
[15，25）4
[25，35）8
[35，45）12
[45，55）5
[55，65）2
[65，75]2
（1）求月收入在百元内的频率，并补全这个频率分布直方图，在图中标出相应的纵坐标；
（2）根据频率分布直方图估计这50人的平均月收入；
（3）为了这个改革方案能够更好的实施，从这些调查者中选取代表提供建议，若从月收入在[35，45）百元和[65，75]百元的不赞成的被调查者中随机抽取2人，求这两名代表月收入差不超过1000元的概率．
19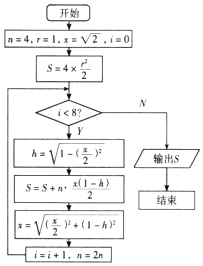．我国魏晋时期的数学家刘徽，他在注《九章算术》中采用正多边形面积逐渐逼近圆面积的算法计算圆周率π，用刘徽自己的原话就是“割之弥细，所失弥少，割之又割，以至于不可割，则与圆合体而无所失矣．”设计程序框图是计算圆周率率不足近似值的算法，其中圆的半径为1．请问程序中输出的S是圆的内接正（　　）边形的面积．
A．1024B．2048C．3072D．1536
16．已知函数f（x）=alnx-x-$\frac{a}{x}$+2a（其中a为常数，a∈R）．
（Ⅰ）求函数f（x）的单调区间；
（Ⅱ）当a＞0时，是否存在实数a，使得当x∈[1，e]时，不等式f（x）＞0恒成立？如果存在，求a的取值范围；如果不存在，说明理由（其中e是自然对数的底数，e=2.71828…）
16．已知焦点在x轴上的椭圆的离心率为$\frac{1}{2}$，且它的长轴长等于4，则椭圆的标准方程是（　　）
A．$\frac{x^2}{4}+\frac{y^2}{3}$=1B．$\frac{x^2}{16}+\frac{y^2}{12}=1$C．$\frac{x^2}{4}+{y^2}=1$D．$\frac{x^2}{16}+\frac{y^2}{4}=1$

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网