题目内容
16.已知焦点在x轴上的椭圆的离心率为$\frac{1}{2}$,且它的长轴长等于4,则椭圆的标准方程是( )| A. | $\frac{x^2}{4}+\frac{y^2}{3}$=1 | B. | $\frac{x^2}{16}+\frac{y^2}{12}=1$ | C. | $\frac{x^2}{4}+{y^2}=1$ | D. | $\frac{x^2}{16}+\frac{y^2}{4}=1$ |
分析 由题意设出椭圆方程并求得a值,再由离心率求得c,结合隐含条件求得b,则椭圆方程可求.
解答 解:由题意可设椭圆方程为$\frac{{x}^{2}}{{a}^{2}}+\frac{{y}^{2}}{{b}^{2}}=1$(a>b>0).
且2a=4,∴a=2,又$e=\frac{c}{a}=\frac{1}{2}$,
∴c=1,则b2=a2-c2=3.
∴椭圆的标准方程是$\frac{{x}^{2}}{4}+\frac{{y}^{2}}{3}=1$.
故选:A.
点评 本题考查椭圆的简单性质,考查了椭圆方程的求法,是基础题.

练习册系列答案
相关题目
7.已知全集U为实数集,集合A={x|x2-2x-3<0},B={x|x<1},则A∩B为( )
| A. | {x|1≤x<3} | B. | {x|x<3} | C. | {x|x≤-1} | D. | {x|-1<x<1} |
8.已知函数f(x)=$\left\{\begin{array}{l}{lo{g}_{\frac{1}{3}}x,x>0}\\{{3}^{x},x≤0}\end{array}\right.$,则f(f(9))的值为( )
| A. | -$\frac{1}{9}$ | B. | -9 | C. | $\frac{1}{9}$ | D. | 9 |
4.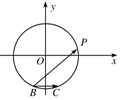 已知△ABC中,BC=1,AB=$\sqrt{3}$,AC=$\sqrt{6}$,点P是△ABC的外接圆上的一个动点,则$\overrightarrow{BP}$•$\overrightarrow{BC}$的最大值是( )
已知△ABC中,BC=1,AB=$\sqrt{3}$,AC=$\sqrt{6}$,点P是△ABC的外接圆上的一个动点,则$\overrightarrow{BP}$•$\overrightarrow{BC}$的最大值是( )
 已知△ABC中,BC=1,AB=$\sqrt{3}$,AC=$\sqrt{6}$,点P是△ABC的外接圆上的一个动点,则$\overrightarrow{BP}$•$\overrightarrow{BC}$的最大值是( )
已知△ABC中,BC=1,AB=$\sqrt{3}$,AC=$\sqrt{6}$,点P是△ABC的外接圆上的一个动点,则$\overrightarrow{BP}$•$\overrightarrow{BC}$的最大值是( )| A. | 2 | B. | $\sqrt{3}$ | C. | $\sqrt{2}$ | D. | $\sqrt{3}+1$ |
8.一个圆柱的正视图是面积为6的矩形,它的侧面积为( )
| A. | 8π | B. | 6π | C. | 4π | D. | 3π |
5.设复数$z=\frac{{2{i^3}}}{i-1}$(i为虚数单位),z则的虚部为( )
| A. | i | B. | -i | C. | -1 | D. | 1 |