题目内容
1.若$\overrightarrow{a}$=(2,-1),$\overrightarrow{b}$=(3,4),则$\overrightarrow{a}$与$\overrightarrow{b}$夹角的余弦值( )| A. | $-\frac{{2\sqrt{5}}}{25}$ | B. | $\frac{{2\sqrt{5}}}{25}$ | C. | $2\sqrt{5}$ | D. | $\frac{{\sqrt{5}}}{5}$ |
分析 根据题意,设$\overrightarrow{a}$与$\overrightarrow{b}$夹角为θ,由向量$\overrightarrow{a}$与$\overrightarrow{b}$的坐标计算可得|$\overrightarrow{a}$|、|$\overrightarrow{b}$|以及$\overrightarrow{a}$•$\overrightarrow{b}$的值,进而由cosθ=$\frac{\overrightarrow{a}•\overrightarrow{b}}{|\overrightarrow{a}||\overrightarrow{b}|}$计算可得答案.
解答 解:根据题意,设$\overrightarrow{a}$与$\overrightarrow{b}$夹角为θ,
若$\overrightarrow{a}$=(2,-1),$\overrightarrow{b}$=(3,4),
则|$\overrightarrow{a}$|=$\sqrt{5}$,|$\overrightarrow{b}$|=5,$\overrightarrow{a}$•$\overrightarrow{b}$=2×3+(-1)×4=2,
cosθ=$\frac{\overrightarrow{a}•\overrightarrow{b}}{|\overrightarrow{a}||\overrightarrow{b}|}$=$\frac{2}{5\sqrt{5}}$=$\frac{2\sqrt{5}}{25}$;
故选:B.
点评 本题考查向量的数量积的运算,关键是掌握向量的坐标计算公式.

练习册系列答案
相关题目
13.已知函数f(x)=e|x|,则$\int_{-2}^4{f(x)}dx$( )
| A. | e4+e2-2 | B. | e4-e2 | C. | e4-e2+2 | D. | e4-e2-2 |
11.设a是实数,且$\frac{2a}{1+i}$+1+i是实数,则a=( )
| A. | $\frac{1}{2}$ | B. | 1 | C. | $\frac{3}{2}$ | D. | -1 |
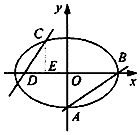 已知椭圆$\frac{x^2}{a^2}+\frac{y^2}{b^2}$(a>b>0)的离心率$e=\frac{{\sqrt{6}}}{3}$,直线AB分别交椭圆下顶点A(0,-1)和右顶点B.
已知椭圆$\frac{x^2}{a^2}+\frac{y^2}{b^2}$(a>b>0)的离心率$e=\frac{{\sqrt{6}}}{3}$,直线AB分别交椭圆下顶点A(0,-1)和右顶点B.