题目内容
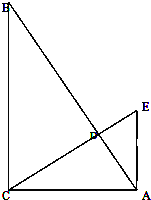 △ABC中,∠BCA=90°,AB=1,过C作CD⊥AB于D,过A作AE⊥AC,CD的延长线交AE于E,设∠B=θ,θ是变量.
△ABC中,∠BCA=90°,AB=1,过C作CD⊥AB于D,过A作AE⊥AC,CD的延长线交AE于E,设∠B=θ,θ是变量.(1)求证:CD-DE=tanθ•cos2θ;
(2)记y=
| 6 |
| 5 |
考点:三角函数中的恒等变换应用
专题:计算题,证明题,三角函数的求值,三角函数的图像与性质
分析:(1)运用解直角三角形的知识,锐角三角函数的定义,求得CD,DE,再由二倍角公式和同角公式化简即可得证;
(2)求出函数y的解析式,运用换元法令t=sinθ+cosθ,求出t的范围,两边平方,可得t的函数式,运用二次函数的最值求法,即可得到所求最值.
(2)求出函数y的解析式,运用换元法令t=sinθ+cosθ,求出t的范围,两边平方,可得t的函数式,运用二次函数的最值求法,即可得到所求最值.
解答:
(1)证明: CD=BCsinθ=ABcosθsinθ=sinθcosθ,
CD=BCsinθ=ABcosθsinθ=sinθcosθ,
DE=ADtanθ=CAsinθtanθ=ABsin2θtanθ=sin2θtanθ,
CD-DE=sinθcosθ-sin2θtanθ=tanθ(cos2θ-sin2θ)=tanθ•cos2θ;
(2)解:y=
(CA+CB)-CD=
(sinθ+cosθ)-sinθcosθ
=
(sinθ+cosθ)-
,
令t=sinθ+cosθ=
sin(θ+
),
由于0<θ<
,则
<θ+
<
,则1<t≤
,
则y=
t-
=-
(t-
)2+
.
当t=
时,y取得最大值
;
当t=
时,y取得最小值为
-
.
 CD=BCsinθ=ABcosθsinθ=sinθcosθ,
CD=BCsinθ=ABcosθsinθ=sinθcosθ,DE=ADtanθ=CAsinθtanθ=ABsin2θtanθ=sin2θtanθ,
CD-DE=sinθcosθ-sin2θtanθ=tanθ(cos2θ-sin2θ)=tanθ•cos2θ;
(2)解:y=
| 6 |
| 5 |
| 6 |
| 5 |
=
| 6 |
| 5 |
| (sinθ+cosθ)2-1 |
| 2 |
令t=sinθ+cosθ=
| 2 |
| π |
| 4 |
由于0<θ<
| π |
| 2 |
| π |
| 4 |
| π |
| 4 |
| 3π |
| 4 |
| 2 |
则y=
| 6 |
| 5 |
| t2-1 |
| 2 |
| 1 |
| 2 |
| 6 |
| 5 |
| 61 |
| 50 |
当t=
| 6 |
| 5 |
| 61 |
| 50 |
当t=
| 2 |
6
| ||
| 5 |
| 1 |
| 2 |
点评:本题考查三角函数的化简和求值,考查二倍角公式及两角和的正弦公式的运用,考查换元法的运用,考查二次函数的最值求法,考查运算能力,属于中档题和易错题.

练习册系列答案
相关题目
命题p:在△ABC中,AB=5,sinC=
,BC=6,则tanA=
;命题q:设函数f(x)=
,若函数g(x)=f(x)-ax(-2≤x≤2)为偶函数,则a=
,则下列命题为真命题的是( )
| 2 |
| 3 |
| 4 |
| 3 |
|
| 1 |
| 2 |
| A、p且q |
| B、p或(¬q) |
| C、(¬p)且q |
| D、p且(¬q) |
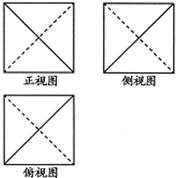 某几何体的三视图如图所示,正视图、侧视图、俯视图都是边长为1的正方形,则此几何体的外接球的表面积为( )
某几何体的三视图如图所示,正视图、侧视图、俯视图都是边长为1的正方形,则此几何体的外接球的表面积为( )| A、3π | ||
| B、4π | ||
| C、2π | ||
D、
|
设某大学的女生体重y(单位:kg)与身高x(单位:cm)具有线性相关关系,根据一组样本数据(xi,yi)(i=1,2,…,n),用最小二乘法建立的回归方程为
=0.85x-85.71,则下列结论中不正确的是( )
 |
| y |
| A、若该大学某女生身高为170cm,则可断定其体重必为58.79kg | ||||
B、回归直线过样本点的中心(
| ||||
| C、若该大学某女生身高增加1cm,则其体重约增加0.85kg | ||||
| D、y与x具有正的线性相关关系 |