题目内容
|2x+2|-|2x-2|≤a恒成立，则实数a的取值范围是（ ）
| A、（-∞，-4） |
| B、[4，+∞） |
| C、[-4，+∞） |
| D、（-4，+∞） |
考点：绝对值三角不等式
专题：计算题,不等式的解法及应用
分析：利用绝对值三角不等式可得（|2x+2|-|2x-2|）max=4，依题意知，a≥（|2x+2|-|2x-2|）max，从而可得答案．
解答：
解：因为|2x+2|-|2x-2|≤|（2x+2）+（2-2x）|=4，即（|2x+2|-|2x-2|）max=4，
又不等式|2x+2|-|2x-2|≤a对于任意实数x恒成立，
所以a≥（|2x+2|-|2x-2|）max=4，
故选：B．
又不等式|2x+2|-|2x-2|≤a对于任意实数x恒成立，
所以a≥（|2x+2|-|2x-2|）max=4，
故选：B．
点评：本题考查绝对值不等式的解法，突出考查绝对值三角不等式的应用，求得（|2x+2|-|2x-2|）max=4是关键，属于中档题．
练习册系列答案
全能测控期末小状元系列答案
相关题目
对于函数f（x）定义域中任意的x1，x2（x1≠x2）有如下结论
①f（x1+x2）=f（x1）•f（x2）
②f（x1•x2）=f（x1）+f（x2）
③
＜0
④f(
)＞
当f（x）=log3x时，上述结论中正确的序号是（ ）
①f（x1+x2）=f（x1）•f（x2）
②f（x1•x2）=f（x1）+f（x2）
③
| f(x1)-f(x2) |
| x1-x2 |
④f(
| x1+x2 |
| 2 |
| f(x1)+f(x2) |
| 2 |
当f（x）=log3x时，上述结论中正确的序号是（ ）
| A、①② | B、②④ | C、①③ | D、③④ |
等差数列{an}的前n项和为Sn．且S3=6，a3=0，则公差d等于（ ）
| A、2 | B、1 | C、-1 | D、-2 |
在△ABC中，a，b，c分为为∠A，∠B，∠C所对的边，若函数f（x）=
x3+bx2+（a2+c2-ac）x+1有极值点，则∠B的范围是（ ）
| 1 |
| 3 |
A、（0，
| ||
B、（0，
| ||
C、[
| ||
D、（
|
计算（1+i）2=（ ）
| A、2i | B、-2i |
| C、2+2i | D、2-2i |
下面的流程图表示的算法执行的结果是（ ）
| A、5050 | B、2550 |
| C、2450 | D、2500 |
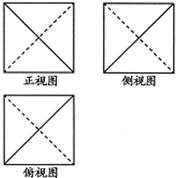某几何体的三视图如图所示，正视图、侧视图、俯视图都是边长为1的正方形，则此几何体的外接球的表面积为（ ）| A、3π | ||
| B、4π | ||
| C、2π | ||
D、
|
已知等差数列{an}，a1=1，a3=3，则数列{
}的前10项和为（ ）
| 1 |
| anan+1 |
A、
| ||
B、
| ||
C、
| ||
D、
|