题目内容
如果对定义在R上的函数f（x），对任意两个不相等的实数x1，x2，都有x1（f（x1）-f（x2））＞x2（f（x1）-f（x2）），则称函数f（x）为“H函数”．下列函数是“H函数”的是（ ）
| A、y=x2 |
| B、y=-ex+1 |
| C、y=2x-sinx |
| D、y=lg|x| |
考点：利用导数研究函数的单调性
专题：导数的概念及应用
分析：不等式x1f（x1）+x2f（x2）＞x1f（x2）+x2f（x1）等价为（x1-x2）[f（x1）-f（x2）]＞0，即满足条件的函数为单调递增函数，判断函数的单调性即可得到结论．
解答：
解：∵对于任意给定的不等实数x1，x2，不等式x1（f（x1）-f（x2））＞x2（f（x1）-f（x2））恒成立，
∴不等式等价为（x1-x2）[f（x1）-f（x2）]＞0恒成立，
即函数f（x）是定义在R上的增函数．
对于A：函数y=x2在定义域上不单调．不满足条件．
对于B：y=-ex+1为减函数，不满足条件．
对于C：y=2x-sinx，y′=2-cosx＞0，函数单调递增，满足条件．
对于D：y=lg|x|在定义域上不单调，不满足条件，
故选：C．
∴不等式等价为（x1-x2）[f（x1）-f（x2）]＞0恒成立，
即函数f（x）是定义在R上的增函数．
对于A：函数y=x2在定义域上不单调．不满足条件．
对于B：y=-ex+1为减函数，不满足条件．
对于C：y=2x-sinx，y′=2-cosx＞0，函数单调递增，满足条件．
对于D：y=lg|x|在定义域上不单调，不满足条件，
故选：C．
点评：本题主要考查函数单调性的应用，将条件转化为函数的单调性的形式是解决本题的关键．
练习册系列答案
相关题目
命题“若α=
，则tanα=1”的逆否命题是（ ）
| π |
| 4 |
A、若α≠
| ||
B、若α=
| ||
C、若tanα≠1，则α=
| ||
D、若tanα≠1，则α≠
|
计算（1+i）2=（ ）
| A、2i | B、-2i |
| C、2+2i | D、2-2i |
下面的流程图表示的算法执行的结果是（ ）
| A、5050 | B、2550 |
| C、2450 | D、2500 |
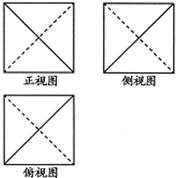某几何体的三视图如图所示，正视图、侧视图、俯视图都是边长为1的正方形，则此几何体的外接球的表面积为（ ）| A、3π | ||
| B、4π | ||
| C、2π | ||
D、
|
向量
=（-1，1），且
与
+2
方向相同，则
•
的范围是（ ）
| a |
| a |
| a |
| b |
| a |
| b |
| A、（1，+∞） |
| B、（-1，1） |
| C、（-1，+∞） |
| D、（-∞，1） |