题目内容
f(x)满足对一切实数,恒有f(x)+f(-x)=x2且在(-∞,0)上单调递增,若f(2-a)-f(a)>2-2a,求a的取值范围.
考点:函数单调性的性质,函数解析式的求解及常用方法
专题:函数的性质及应用,不等式的解法及应用
分析:由条件可令f(x)=g(x)+kx2,求出k,及g(x)的奇偶性,再由f(x)在(-∞,0)上单调递增,通过导数求得g(x)的单调性,再由f(2-a)-f(a)>2-2a,即为f(2-a)-
>f(a)-
,即有g(2-a)>g(a),通过单调性即可解得a的范围.
| (2-a)2 |
| 2 |
| a2 |
| 2 |
解答:
解:由于f(x)+f(-x)=x2,
可令f(x)=g(x)+kx2,
即有g(x)+kx2+g(-x)+kx2=x2恒成立,
则2k=1,g(-x)+g(x)=0,
则有k=
,g(x)为奇函数.
即有g(x)=f(x)-
x2,
当x<0时,g′(x)=f′(x)-x,由f(x)递增,
则f′(x)>0,g′(x)>0,
则有g(x)在x<0递增,且g(0)=0,
由于g(x)为奇函数,则g(x)在R上递增.
f(2-a)-f(a)>2-2a,即为
f(2-a)-
>f(a)-
,
即有g(2-a)>g(a),
则有2-a>a,解得a<1,
故a的取值范围是(-∞,1).
可令f(x)=g(x)+kx2,
即有g(x)+kx2+g(-x)+kx2=x2恒成立,
则2k=1,g(-x)+g(x)=0,
则有k=
| 1 |
| 2 |
即有g(x)=f(x)-
| 1 |
| 2 |
当x<0时,g′(x)=f′(x)-x,由f(x)递增,
则f′(x)>0,g′(x)>0,
则有g(x)在x<0递增,且g(0)=0,
由于g(x)为奇函数,则g(x)在R上递增.
f(2-a)-f(a)>2-2a,即为
f(2-a)-
| (2-a)2 |
| 2 |
| a2 |
| 2 |
即有g(2-a)>g(a),
则有2-a>a,解得a<1,
故a的取值范围是(-∞,1).
点评:本题考查函数的性质和运用,主要考查函数的奇偶性和单调性的运用解不等式,构造函数g(x)=f(x)-
x2,求出单调性是解题的关键.
| 1 |
| 2 |

练习册系列答案
相关题目
若函数f(x)在x=a处有导数,则
为( )
| lim |
| h→a |
| f(h)-f(a) |
| h-a |
| A、f(a) | B、f′(a) |
| C、f′(h) | D、f(h) |
已知S、A、B、C是球O表面上的点,SA⊥平面ABC,△ABC为等边三角形,SA=AB=1,则球O的表面积为( )
A、
| ||
B、
| ||
| C、π | ||
D、
|
给定△ABC,若点D满足
=
,
=
+λ
,则λ等于( )
| AD |
| 2 |
| 3 |
| AB |
| CD |
| 1 |
| 3 |
| CA |
| CB |
A、
| ||
B、
| ||
C、-
| ||
D、-
|
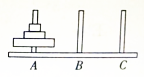 从古印度的汉诺塔传说演变了一个汉诺塔游戏:如图,有三根杆子A、B、C,A杆上有三个碟子(大小不等,自上到下,由小到大),每次移动一个碟子,小的只能叠在大的上面,把所有的碟子从A杆移到C杆上,试设计一个算法,完成上述游戏.
从古印度的汉诺塔传说演变了一个汉诺塔游戏:如图,有三根杆子A、B、C,A杆上有三个碟子(大小不等,自上到下,由小到大),每次移动一个碟子,小的只能叠在大的上面,把所有的碟子从A杆移到C杆上,试设计一个算法,完成上述游戏.