题目内容
14.在△ABC中,角A,B,C的对边分别为a,b,c.已知A=45°,cosB=$\frac{4}{5}$.(1)求cosC的值;
(2)若BC=20,D为AB的中点,求CD的长.
分析 (1)cosC=cos(π-A-B)=-cos(A+B)=-cosAcosB+sinAsinB即可求解.
(2)由正弦定理得$\frac{BC}{sinA}=\frac{AC}{sinB}$⇒AC=12$\sqrt{2}$,由D为AB的中点,⇒${\overrightarrow{CD}}^{2}=\frac{1}{4}({\overrightarrow{CA}}^{2}+{\overrightarrow{CB}}^{2}+2\overrightarrow{CA}•\overrightarrow{CB})$=$\frac{1}{4}(288+400+2×12\sqrt{2}×20×(-\frac{\sqrt{2}}{10})$=592,即可求得CD
解答 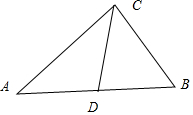 解:(1)在△ABC中,由cosB=$\frac{4}{5}$.得sinB=$\frac{3}{5}$,
解:(1)在△ABC中,由cosB=$\frac{4}{5}$.得sinB=$\frac{3}{5}$,
则cosC=cos(π-A-B)=-cos(A+B)=-cosAcosB+sinAsinB=-$\frac{\sqrt{2}}{2}×\frac{4}{5}+\frac{\sqrt{2}}{2}×\frac{3}{5}=-\frac{\sqrt{2}}{10}$.
(2)在△ABC中,∵sinB=$\frac{3}{5}$,A=45°,BC=20,
由正弦定理得$\frac{BC}{sinA}=\frac{AC}{sinB}$⇒AC=12$\sqrt{2}$,
∵D为AB的中点,∴$\overrightarrow{CD}=\frac{1}{2}(\overrightarrow{CA}+\overrightarrow{CB})$⇒${\overrightarrow{CD}}^{2}=\frac{1}{4}({\overrightarrow{CA}}^{2}+{\overrightarrow{CB}}^{2}+2\overrightarrow{CA}•\overrightarrow{CB})$=$\frac{1}{4}(288+400+2×12\sqrt{2}×20×(-\frac{\sqrt{2}}{10})$=592,
∴CD=4$\sqrt{37}$.
点评 本题考查了三角恒等变形,正弦定理,考查了计算能力,属于中档题.

 字词句段篇系列答案
字词句段篇系列答案| A. | $\frac{2}{3}\overrightarrow a+\frac{1}{3}\overrightarrow b$ | B. | $\frac{1}{3}\overrightarrow a+\frac{2}{3}\overrightarrow b$ | C. | $\frac{1}{3}\overrightarrow a+\frac{1}{3}\overrightarrow b$ | D. | $\frac{1}{2}\overrightarrow a+\frac{1}{2}\overrightarrow b$ |
| A. | $\frac{3π}{4}$ | B. | $\frac{π}{4}$ | C. | $\frac{2π}{3}$ | D. | $\frac{5π}{6}$ |
| A. | f(x)=1,g(x)=x0 | B. | f(x)=x2,g(x)=(x+1)2 | ||
| C. | f(x)=x,g(x)=elnx | D. | f(x)=|x|,g(x)=$\left\{\begin{array}{l}{x,}&{x≥0}\\{-x,}&{x<0}\end{array}\right.$ |
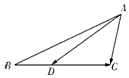 如图,在△ABC中,∠BAC=60°,AB=2,AC=1,D是BC边上一点,且$\overrightarrow{CD}$=2$\overrightarrow{DB}$,则$\overrightarrow{AD}$•$\overrightarrow{BC}$ 的值为-2.
如图,在△ABC中,∠BAC=60°,AB=2,AC=1,D是BC边上一点,且$\overrightarrow{CD}$=2$\overrightarrow{DB}$,则$\overrightarrow{AD}$•$\overrightarrow{BC}$ 的值为-2.