题目内容
已知数列{an}中,a1=1,对任意的k∈N*,a2k-1、a2k、a2k+1成等比数列,公比为qk;a2k、a2k+1、a2k+2成等差数列,公差为dk,且d1=2.
(1)写出数列{an}的前四项;
(2)设bk=
,求数列{bk}的通项公式;
(3)求数列{dk}的前k项和Dk.
(1)写出数列{an}的前四项;
(2)设bk=
| 1 |
| qk-1 |
(3)求数列{dk}的前k项和Dk.
考点:等差数列与等比数列的综合
专题:综合题,等差数列与等比数列
分析:(1)由题意得
,求出a2=2或a2=-1,即可写出数列{an}的前四项;
(2)由a2k,a2k+1,a2k+2成等差数列,其公差为dk,知2a2k+1=a2k+a2k+2,从而能够证明{bk}是等差数列,且公差为1.
(3)由d1=2,得a3=a2+2,解得a2=2,或a2=-1.由此进行分类讨论,能够求出Dk.
|
(2)由a2k,a2k+1,a2k+2成等差数列,其公差为dk,知2a2k+1=a2k+a2k+2,从而能够证明{bk}是等差数列,且公差为1.
(3)由d1=2,得a3=a2+2,解得a2=2,或a2=-1.由此进行分类讨论,能够求出Dk.
解答:
解:(1)由题意得
,∴a22=a2+2,a2=2或a2=-1.…(2分)
故数列{an}的前四项为1,2,4,6或1,-1,1,3.…(4分)
(2)∵a2k-1,a2k,a2k+1成公比为qk的等比数列,a2k+1,a2k+2,a2k+3成公比为qk+1的等比数列,
∴a2k+1=a2kqk,a2k+2=a2k+1qk+1
又∵a2k,a2k+1,a2k+2成等差数列,
∴2a2k+1=a2k+a2k+2.
得2a2k+1=
+a2k+1qk+1,2=
+qk+1,…(6分)
∴
=qk+1-1,
∴
=
=1+
,
-
=1,即bk+1-bk=1.
∴数列{bk}为公差d=1等差数列,且b1=
=1或b1=
=-
.…(8分)
∴bk=b1+(k-1)•1=k或bk=k-
.…(10分)
(3)当b1=1时,由(2)得bk=
=k,qk=
.
=(
)2,a2k+1=
•
…
•a1=(
)2•(
)2…(
)2•1=(k+1)2,a2k=
=k(k+1),dk=a2k+1-a2k=
=k+1,Dk=
.…(13分)
当b1=-
时,同理可得dk=4k-2,Dk=2k2.…(16分)
|
故数列{an}的前四项为1,2,4,6或1,-1,1,3.…(4分)
(2)∵a2k-1,a2k,a2k+1成公比为qk的等比数列,a2k+1,a2k+2,a2k+3成公比为qk+1的等比数列,
∴a2k+1=a2kqk,a2k+2=a2k+1qk+1
又∵a2k,a2k+1,a2k+2成等差数列,
∴2a2k+1=a2k+a2k+2.
得2a2k+1=
| a2k+1 |
| qk |
| 1 |
| qk |
∴
| qk-1 |
| qk |
∴
| 1 |
| qk+1-1 |
| qk |
| qk-1 |
| 1 |
| qk-1 |
| 1 |
| qk+1-1 |
| 1 |
| qk-1 |
∴数列{bk}为公差d=1等差数列,且b1=
| 1 |
| q1-1 |
| 1 |
| q1-1 |
| 1 |
| 2 |
∴bk=b1+(k-1)•1=k或bk=k-
| 3 |
| 2 |
(3)当b1=1时,由(2)得bk=
| 1 |
| qk-1 |
| k+1 |
| k |
| a2k+1 |
| a2k-1 |
| k+1 |
| k |
| a2k+1 |
| a2k-1 |
| a2k-1 |
| a2k-3 |
| a3 |
| a1 |
| k+1 |
| k |
| k |
| k-1 |
| 2 |
| 1 |
| a2k+1 |
| qk |
| a2k+1 |
| qk |
| k(k+3) |
| 2 |
当b1=-
| 1 |
| 2 |
点评:本题考查数列的前n项和的计算,等差数列的证明,综合性强,难度大,是高考的重点.解题时要认真审题,仔细解答,注意计算能力的培养.

练习册系列答案
相关题目
 任意画一个正方形,再将这个正方形各边的中点相连得到第二个正方形,依此类推,这样一共画了3个正方形,如图所示.若向图形中随机投一点,则所投点落在第三个正方形的概率是( )
任意画一个正方形,再将这个正方形各边的中点相连得到第二个正方形,依此类推,这样一共画了3个正方形,如图所示.若向图形中随机投一点,则所投点落在第三个正方形的概率是( )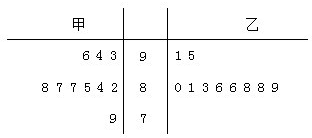
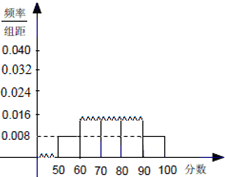 随机抽取某中学高一级学生的一次数学统测成绩得到一样本,其分组区间和频数是:[50,60),2;[60,70),7;[70,80),10;[80,90),x;[90,100],2.其频率分布直方图受到破坏,可见部分如图所示,据此解答如下问题.
随机抽取某中学高一级学生的一次数学统测成绩得到一样本,其分组区间和频数是:[50,60),2;[60,70),7;[70,80),10;[80,90),x;[90,100],2.其频率分布直方图受到破坏,可见部分如图所示,据此解答如下问题.