题目内容
已知方程x2+y2+kx+2y+k2=0所表示的圆有最大面积，则椭圆
+
=1的长轴长为（ ）
| x2 |
| 1+k |
| y2 |
| 2-k |
| A、4 | ||
| B、2 | ||
C、2
| ||
| D、与k有关 |
考点：椭圆的简单性质
专题：圆锥曲线的定义、性质与方程
分析：在圆x2+y2+kx+2y+k2=0中，r=
=
≤2，所以当方程x2+y2+kx+2y+k2=0所表示的圆有最大面积时，k=0，由此能求出椭圆
+
=1的长轴长．
| k2+4-4k2 |
| 4-3k2 |
| x2 |
| 1+k |
| y2 |
| 2-k |
解答：
解：∵圆x2+y2+kx+2y+k2=0中，
∴r=
=
≤2，
∴当方程x2+y2+kx+2y+k2=0所表示的圆有最大面积时，k=0，
此时椭圆
+
=1简化为：x2 +
=1，
其长轴长为2a=2
．
故选：C．
∴r=
| k2+4-4k2 |
| 4-3k2 |
∴当方程x2+y2+kx+2y+k2=0所表示的圆有最大面积时，k=0，
此时椭圆
| x2 |
| 1+k |
| y2 |
| 2-k |
| y2 |
| 2 |
其长轴长为2a=2
| 2 |
故选：C．
点评：本题考查椭圆的长轴长的求法，是基础题，解题时要认真审题，注意圆的性质的灵活运用．
练习册系列答案
相关题目
函数f（x）的定义域为D，满足：①f（x）在D内是单调函数；②存在[
，
]⊆D，使得f（x）在[
，
]上的值域为[a，b]，那么就称函数y=f（x）为“优美函数”，若函数f（x）=logc（cx-t）（c＞0，c≠1）是“优美函数”，则t的取值范围为（ ）
| a |
| 2 |
| b |
| 2 |
| a |
| 2 |
| b |
| 2 |
| A、（0，1） | ||
B、（0，
| ||
C、（-∞，
| ||
D、（0，
|
直线m、n和平面a、β．下列四个命题中，
①若m∥a，n∥a，则m∥n；
②若m?α，n?α，m∥β，n∥β，则α∥β；
③若α⊥β，m?α，则m⊥β；
④若α⊥β，m⊥β，m?α，则m∥α，
其中正确命题的个数是（ ）
①若m∥a，n∥a，则m∥n；
②若m?α，n?α，m∥β，n∥β，则α∥β；
③若α⊥β，m?α，则m⊥β；
④若α⊥β，m⊥β，m?α，则m∥α，
其中正确命题的个数是（ ）
| A、0 | B、1 | C、2 | D、3 |
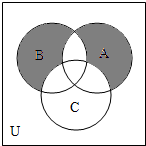如图所示，已知集合A、B、C为全集U的子集，则图中阴影部分所表示的集合为（ ）| A、（∁∪C）∪（A∪B） |
| B、（A∪B）∩[∁∪（A∩B）] |
| C、（A∪B）∩[∁∪（A∩B∩C）] |
| D、{A∩[∁∪（B∪C）]}∪{B∩[∁∪（A∪C）]} |
命题“对任意x∈R，均有x2-2x+5≤0”的否定为（ ）
| A、对任意x∈R，均有x2-2x+5≥0 |
| B、对任意x∉R，均有x2-2x+5≤0 |
| C、存在x∈R，使得x2-2x+5＞0 |
| D、存在x∉R，使得x2-2x+5＞0 |
在如图所示的茎叶图中，中位数和众数分别是（ ）
| A、93，92 |
| B、92，93 |
| C、91，93 |
| D、93，93 |