题目内容
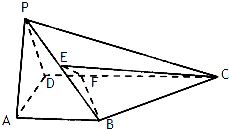 如图,在四棱锥P-ABCD中,AB⊥平面PAD,AB∥CD,△PAD是边长为
如图,在四棱锥P-ABCD中,AB⊥平面PAD,AB∥CD,△PAD是边长为| 2 |
(Ⅰ)证明:EF⊥平面PAB;
(Ⅱ)若FC=2,求点C到平面EBF的距离.
考点:点、线、面间的距离计算,直线与平面垂直的判定
专题:综合题,空间位置关系与距离
分析:(Ⅰ)取PA中点M,连接MD,ME,证明四边形MEDF是平行四边形,可得EF∥MD,再证明MD⊥平面PAB,即可证明EF⊥平面PAB.
(Ⅱ)若FC=2,利用等体积求点C到平面EBF的距离.
(Ⅱ)若FC=2,利用等体积求点C到平面EBF的距离.
解答:
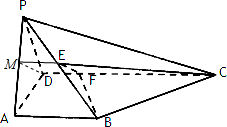 (Ⅰ)证明:如图,取PA中点M,连接MD,ME,
(Ⅰ)证明:如图,取PA中点M,连接MD,ME,
∵E是PB的中点,
∴ME∥AB,ME=
AB,
∵AB=2DF,AB∥CD,
∴ME∥DF,ME=DF
∴四边形MEDF是平行四边形,
∴EF∥MD,
∵PD=AD,∴MD⊥PA,
∵AB⊥平面PAD,∴MD⊥AB,
∵PA∩AB=A,∴MD⊥平面PAB,
∴EF⊥平面PAB.
(Ⅱ)解:由题意,△EBF中,EF=
,EB=
,BF=
,
∴EF2+EB2=BF2,
∴S△EBF=
×
×
=
,
设点C到平面EBF的距离为h,则
∵FC=2,AD=
,∴S△BFC=
,
∵E到平面BFC的距离为
,
∴由等体积可得
×
×
=
×
h,
∴h=
.
 (Ⅰ)证明:如图,取PA中点M,连接MD,ME,
(Ⅰ)证明:如图,取PA中点M,连接MD,ME,∵E是PB的中点,
∴ME∥AB,ME=
| 1 |
| 2 |
∵AB=2DF,AB∥CD,
∴ME∥DF,ME=DF
∴四边形MEDF是平行四边形,
∴EF∥MD,
∵PD=AD,∴MD⊥PA,
∵AB⊥平面PAD,∴MD⊥AB,
∵PA∩AB=A,∴MD⊥平面PAB,
∴EF⊥平面PAB.
(Ⅱ)解:由题意,△EBF中,EF=
| ||
| 2 |
| ||
| 2 |
| 3 |
| 2 |
∴EF2+EB2=BF2,
∴S△EBF=
| 1 |
| 2 |
| ||
| 2 |
| ||
| 2 |
3
| ||
| 8 |
设点C到平面EBF的距离为h,则
∵FC=2,AD=
| 2 |
| 2 |
∵E到平面BFC的距离为
| ||
| 4 |
∴由等体积可得
| 1 |
| 3 |
| 2 |
| ||
| 4 |
| 1 |
| 3 |
3
| ||
| 8 |
∴h=
2
| ||
| 3 |
点评:本题考查直线与平面垂直的证明,求三棱锥的体积,解题时要认真审题,注意合理地化立体几何问题为平面几何问题.

练习册系列答案
相关题目
已知向量
=(1,-2),
=(-
,y),若
∥
,则y=( )
| a |
| b |
| 1 |
| 2 |
| a |
| b |
| A、1 | B、-1 | C、2 | D、-2 |
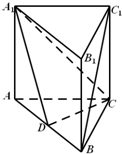 如图,在直三棱柱ABC-A1B1C1中,AC=BC=AA1,∠ACB=90°,点D是AB的中点.
如图,在直三棱柱ABC-A1B1C1中,AC=BC=AA1,∠ACB=90°,点D是AB的中点.