题目内容
在空间直角坐标系中,z轴上到点A(1,0,2)与B(2,-2,1)距离相等的点的坐标为 .
考点:空间两点间的距离公式
专题:空间位置关系与距离
分析:根据点C在z轴上,设出点C的坐标,再根据C到A与到B的距离相等,由空间中两点间的距离公式求得AC,BC,解方程即可求得C的坐标.
解答:
解:设C(0,0,z)
由点C到点A(1,0,2)与点B(2,-2,1)的距离相等,得
12+02+(z-2)2=(2-0)2+(-2-0)2+(z-1)2
解得z=-2,故C(0,0,-2)
故答案为:(0,0,-2).
由点C到点A(1,0,2)与点B(2,-2,1)的距离相等,得
12+02+(z-2)2=(2-0)2+(-2-0)2+(z-1)2
解得z=-2,故C(0,0,-2)
故答案为:(0,0,-2).
点评:考查空间两点间的距离公式,空间两点的距离公式和平面中的两点距离公式相比较记忆,利于知识的系统化,属基础题.

练习册系列答案
 提分百分百检测卷单元期末测试卷系列答案
提分百分百检测卷单元期末测试卷系列答案 小学期末标准试卷系列答案
小学期末标准试卷系列答案
相关题目
如图所示,程序框图(算法流程图)的输出结果是( )


A、
| ||
B、
| ||
C、
| ||
D、
|
已知a=1.270.2,b=log0.3(tan46°),c=2sin29°,则a,b,c的大小关系是( )
| A、a>b>c |
| B、c>a>b |
| C、b>a>c |
| D、a>c>b |
若角α的终边在第二象限,则( )
| A、cosαtanα>0 |
| B、sinαtanα>0 |
| C、sinαcosα>0 |
| D、sinα+cosα>0 |
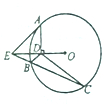 如图,AE是的⊙O切线,A是切点,AD⊥OE于点D,割线EC交⊙O于B,C两点.
如图,AE是的⊙O切线,A是切点,AD⊥OE于点D,割线EC交⊙O于B,C两点.