已知2x+y-2≥0x-2y+4≥03x-y-3≤0.则z=x2-2y2最大值为．题目和参考答案——青夏教育精英家教网—

题目内容

已知

2x+y-2≥0

x-2y+4≥0

3x-y-3≤0

，则z=x²-2y²最大值为

．

考点：简单线性规划

专题：不等式的解法及应用

分析：先画出可行域，然后在本题中要求z=x²-2y²的最大值，则z的几何意义就是表示双曲线中的a²，利用直线和双曲线的位置关系进行求解即可．

解答： 解：作出不等式组对应的平面区域，

先画出可行域，在本题中要求z=x²-2y²的最大值，
则z必然为正的，
则z=x²-2y²等价为

=1，即z=a²，
所以根据图象可知当z=x²-2y²与直线3x-y-3=0相切时z最大，联立方程，
消去y可得17x²-36x+18+z=0，
由△=0，
得（-36）²-4×17×（18+z）=0
解得z=

故答案为

点评：本题主要考查线性规划的应用，利用双曲线的性质结合直线和双曲线的位置关系是解决本题的关键．综合性较强，有一定的难度．

练习册系列答案

68所名校图书小升初高分夺冠真卷系列答案

伴你成长周周练月月测系列答案

小升初金卷导练系列答案

相关题目

已知等差数列{a_n}的公差d不为0，且a₁，a₃，a₇成等比数列，则

的值为

．

已知函数f_n（x）=axⁿ+bx+c（a，b，c∈R），
（Ⅰ）若f₁（x）=3x+1，f₂（x）为偶函数，求a，b，c的值；
（Ⅱ）若对任意实数x，不等式2x≤f₂（x）≤

(x+1)2恒成立，求f₂（-1）的取值范围；
（Ⅲ）当a=1时，对任意x₁，x₂∈[-1，1]，恒有|f₂（x₁）-f₂（x₂）|≤4，求实数b的取值范围．

在空间直角坐标系中，z轴上到点A（1，0，2）与B（2，-2，1）距离相等的点的坐标为

．

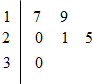某车间共有12名工人，随机抽取6名，他们某日加工零件个数的茎叶图如图所示，其中茎为十位数，叶为个位数．
（1）根据茎叶图计算样本均值；
（2）日加工零件个数大于样本均值的工人为优秀工人，根据茎叶图推断该车间12名工人中有几名优秀工人；
（3）从抽出的6名工人中，任取2人，求恰有1名优秀工人的概率．

给出如下四个命题：
①若“P∨q”为真命题，则p，q均为假命题；
②“若a＞b，则2^a＞2^b-1”的否命题为“若a≤b，则2^a≤2^b-1”
③“?x∈R，x²+x≥1”的否定为“?x₀∈R，x₀²+x₀≤1”；
④“x＞0”是“x+

≥2”的充要条件．
其中不正确的命题序号为

．

已知点A（4，1）、B（0，4），点P在直线l：x+y+1=0上移动，求||PA|-|PB||取最大值时，点P的坐标及这个最大值．

表示的平面区域无公共点，则3a-2b的最小值与最大值的和等于

．

已知函数f（x）是偶函数，而且在上[1，6]是减函数，且有最小值为2，那么在[-6，-1]上说法正确的是（　　）

试题分类