题目内容
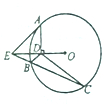如图，AE是的⊙O切线，A是切点，AD⊥OE于点D，割线EC交⊙O于B，C两点．（1）证明：O，D，B，C四点共线；
（2）设∠DBC=50°，∠ODC=30°，求∠OEC的大小．
考点：弦切角,圆內接多边形的性质与判定
专题：选作题,立体几何
分析：（1）连结OA，则OA⊥EA．由已知条件利用射影定理和切割线定理推导出
=
，由此能够证明O，D，B，C四点共圆．
（2）连结OB．∠OEC+∠OCB+∠COE=180°，能求出∠OEC的大小．
| ED |
| BD |
| EC |
| EO |
（2）连结OB．∠OEC+∠OCB+∠COE=180°，能求出∠OEC的大小．
解答：
（1）证明：连结OA，则OA⊥EA．
由射影定理得EA2=ED•EO．
由切割线定理得EA2=EB•EC，
∴ED•EO=EB•EC，即
=
，
又∠OEC=∠OEC，∴△BDE∽△OCE，
∴∠EDB=∠OCE．
∴O，D，B，C四点共圆．…（6分）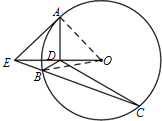
（2）解：连结OB．因为∠OEC+∠OCB+∠COE=180°，
结合（1）得：∠OEC=180°-∠OCB-∠COE
=180°-∠OBC-∠DBE
=180°-∠OBC-（180°-∠DBC）
=∠DBC-∠ODC=20°．
∴∠OEC的大小为20°．…（10分）
由射影定理得EA2=ED•EO．
由切割线定理得EA2=EB•EC，
∴ED•EO=EB•EC，即
| ED |
| BD |
| EC |
| EO |
又∠OEC=∠OEC，∴△BDE∽△OCE，
∴∠EDB=∠OCE．
∴O，D，B，C四点共圆．…（6分）
（2）解：连结OB．因为∠OEC+∠OCB+∠COE=180°，
结合（1）得：∠OEC=180°-∠OCB-∠COE
=180°-∠OBC-∠DBE
=180°-∠OBC-（180°-∠DBC）
=∠DBC-∠ODC=20°．
∴∠OEC的大小为20°．…（10分）
点评：本题考查四点共圆的证明，考查角的大小的求法，是中档题，
练习册系列答案
相关题目
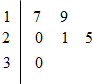某车间共有12名工人，随机抽取6名，他们某日加工零件个数的茎叶图如图所示，其中茎为十位数，叶为个位数．