题目内容

1．设命题P：?x0∈（0，+∞），${3^{x_0}}$＜$x_0^3$，则命题￢p为?x∈（0，+∞），3x≥x3．

分析 利用特称命题的否定是全称命题写出结果即可．

解答 解：因为特称命题的否定是全称命题，所以，命题P：?x0∈（0，+∞），${3^{x_0}}$＜$x_0^3$，则命题￢p为：?x∈（0，+∞），3x≥x3，
故答案为：?x∈（0，+∞），3x≥x3．

点评 本题考查命题的否定，特称命题与全称命题的否定关系，是基础题．

练习册系列答案
相关题目
4．已知函数f（x）是定义在R上的奇函数，且当x＞0时，f（x）=-x2+ax-1-a，若函数f（x）为R上的单调减函数，则a的取值范围是 （　　）
A．a≥-1B．-1≤a≤0C．a≤0D．a≤-1
12．设i是虚数单位，复数$\frac{4i}{1+i}$=（　　）
A．2-2iB．-2-2iC．-2+2iD．2+2i
9．已知2a=3b=m，ab≠0且a，ab，b成等差数列，则m=（　　）
A．$\sqrt{2}$B．$\sqrt{3}$C．$\sqrt{6}$D．6
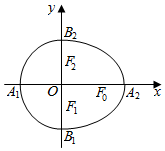16．设函数y=f（x）的图象与y=2x+a的图象关于y=-x+1对称，且f（-3）+f（-7）=1，则a的值为2．
6．已知椭圆$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1（a＞b＞0）的右焦点为F1，左焦点为F2，若椭圆上存在一点P，满足线段PF1相切于椭圆的短轴为直径的圆，切点为线段PF1的中点，则该椭圆的离心率为$\frac{\sqrt{5}}{3}$．
13．我们把由半椭圆$\frac{{x}^{2}}{{a}^{2}}+\frac{{y}^{2}}{{b}^{2}}=1$（x≥0）与半椭圆$\frac{{y}^{2}}{{b}^{2}}+\frac{{x}^{2}}{{c}^{2}}=1$（x≤0）合成的曲线称作“果圆”，其中a2=b2+c2，a＞0，b＞c＞0．如图，点F0，F1，F2是相应椭圆的焦点，A1，A2和B1，B2分别是“果圆”与x，y轴的交点．
（1）若△F0F1F2是边长为1的等边三角形，求“果圆”的方程；
（2）当|A1A2|＞|B1B2|时，求$\frac{b}{a}$的取值范围．
10．已知向量$\overrightarrow{a}$=（1，$\sqrt{3}$），$\overrightarrow{b}$=（0，t2+1），则当$t∈[-\sqrt{3}，2]$时，|$\overrightarrow{a}$-t$\frac{\overrightarrow{b}}{|\overrightarrow{b}|}$|的取值范围是[1，$\sqrt{13}$]．
11．已知△ABC的外接圆的圆心为点O，半径为l，若$\overrightarrow{AB}+\overrightarrow{AC}=2\overrightarrow{AO}$，且|$\overrightarrow{AO}$|=|$\overrightarrow{AC}$|，则$\overrightarrow{BA}•\overrightarrow{BC}$=3．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网