题目内容
6.已知椭圆$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的右焦点为F1,左焦点为F2,若椭圆上存在一点P,满足线段PF1相切于椭圆的短轴为直径的圆,切点为线段PF1的中点,则该椭圆的离心率为$\frac{\sqrt{5}}{3}$.分析 设线段PF1的中点为M,利用OM是△F1PF2的中位线,以及椭圆的定义求出直角三角形OMF1的三边之长,再由勾股定理结合隐含条件求离心率.
解答  解:设线段PF1的中点为M,由题意知,OM=b,又OM是△F1PF2的中位线,
解:设线段PF1的中点为M,由题意知,OM=b,又OM是△F1PF2的中位线,
∴OM=$\frac{1}{2}$PF2=b,则PF2=2b,由椭圆的定义知PF1=2a-PF2=2a-2b,
又MF=$M{F}_{1}=\frac{1}{2}P{F}_{1}$=$\frac{1}{2}$(2a-2b)=a-b,OF1=c,
在直角三角形OMF1中,由勾股定理得:(a-b)2+b2=c2,
又a2-b2=c2,可得2a=3b,
故有4a2=9b2=9(a2-c2),
由此可求得离心率e=$\frac{c}{a}=\frac{\sqrt{5}}{3}$,
故答案为:$\frac{\sqrt{5}}{3}$.
点评 本题考查椭圆的定义,考查椭圆的简单性质,注意椭圆上任一点到两个焦点的距离之和等于常数2a的应用,是中档题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
17.函数f(x)=cos(ωx+φ)的部分图象如图所示,则f(x)的单调递增区间为( )
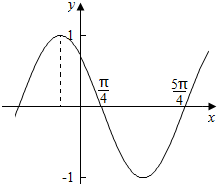

| A. | (kπ+$\frac{3}{4}$π,kπ+$\frac{7}{4}$π),k∈Z | B. | (kπ+$\frac{π}{4}$,kπ+$\frac{5π}{4}$),k∈Z | ||
| C. | (2kπ+$\frac{π}{4}$,2kπ+$\frac{5}{4}$π),k∈Z | D. | (2k+$\frac{3}{4}$π,2k+$\frac{7}{4}$π),k∈Z |
14.阅读如图所示的程序框图,运行相应的程序,若输出的S为$\frac{11}{12}$,则判断框中填写的内容可以是( )


| A. | n<5 | B. | n<6 | C. | n≤6 | D. | n<9 |
18.已知集合A={x|0≤x≤4},B={0,1,2},则A∩B中的元素个数为( )
| A. | 2 | B. | 3 | C. | 4 | D. | 5 |
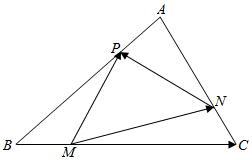 如图,M、N、P分别是三角形ABC三边BC、CA、AB上的点,且满足$\frac{AP}{AB}=\frac{BM}{BC}=\frac{CN}{CA}=\frac{1}{4}$,设$\overrightarrow{AB}$=$\overrightarrow{a}$,$\overrightarrow{AC}$=$\overrightarrow{b}$.
如图,M、N、P分别是三角形ABC三边BC、CA、AB上的点,且满足$\frac{AP}{AB}=\frac{BM}{BC}=\frac{CN}{CA}=\frac{1}{4}$,设$\overrightarrow{AB}$=$\overrightarrow{a}$,$\overrightarrow{AC}$=$\overrightarrow{b}$.