题目内容
16.设函数y=f(x)的图象与y=2x+a的图象关于y=-x+1对称,且f(-3)+f(-7)=1,则a的值为2.分析 先求出函数y=f(x)的解析式,再由f(-3)+f(-7)=1,问题得以解决.
解答 解:设函数y=f(x)的任意点的坐标为(x,y),关于y=-x+1对称点的坐标(m,n),则(m,n)在
y=2x+a的图象上,$\left\{\begin{array}{l}{\frac{y+n}{2}=-\frac{x+m}{2}+1}\\{\frac{y-n}{x-m}=1}\end{array}\right.$,
解得m=1-y,n=1-x,
代入y=2x+a可得:1-x=21-y+a,
即:y=log2(1-x)-a-1,函数y=f(x)=log2(1-x)-a-1,
∵f(-3)+f(-7)=1,
∴log24-a-1+log28-a-1=1,
解得,a=2,
故答案为:2.
点评 本题考查函数与方程的综合应用,对称知识的应用,函数的解析式的求法,属于中档题.

练习册系列答案
相关题目
19.将函数f(x)=2sin(2x+$\frac{π}{4}$)的图象向右平移$\frac{π}{6}$,得到函数g(x)的图象,则g($\frac{π}{4}$)=( )
| A. | $\frac{\sqrt{6}-\sqrt{2}}{2}$ | B. | $\frac{\sqrt{6}-\sqrt{2}}{4}$ | C. | $\frac{\sqrt{6}+\sqrt{2}}{2}$ | D. | $\frac{\sqrt{6}+\sqrt{2}}{4}$ |
4.已知集合A={x|x2-3x+2<0},B={x|log4x>$\frac{1}{2}$},则( )
| A. | A⊆B | B. | B⊆A | C. | A∩∁RB=R | D. | A∩B=∅ |
11.若全集U={0,1,2,4},且∁UA={1,2},则集合A=( )
| A. | {1,4} | B. | {0,4} | C. | {2,4} | D. | {0,2} |
8.椭圆x2+$\frac{{y}^{2}}{4}$=1短轴的左右两个端点分别为A,B,直线l过定点(0,1)交椭圆于两点C,D.设直线AD,CB的斜率分别为k1,k2,若k1:k2=2:1,则直线l斜率k的值为( )
| A. | k=2 | B. | k=3 | C. | .k=$\frac{1}{3}$或3 | D. | k=2或$\frac{1}{2}$ |
5.复数z1,z2在复平面内对应的点关于直线y=x对称,且z1=3+2i,则z1•z2=( )
| A. | 12+13i | B. | 13+12i | C. | -13i | D. | 13i |
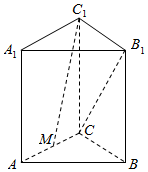 如图,在直三棱柱ABC-A1B1C1中,AB=BC=CC1=2,AC=2$\sqrt{3}$,M是AC的中点,则异面直线CB1与C1M所成角的余弦值为$\frac{\sqrt{14}}{28}$.
如图,在直三棱柱ABC-A1B1C1中,AB=BC=CC1=2,AC=2$\sqrt{3}$,M是AC的中点,则异面直线CB1与C1M所成角的余弦值为$\frac{\sqrt{14}}{28}$.